How to Calculate Present Value

Present value is a critical financial concept.

Investors calculate the present value (PV) of future payments when evaluating a mortgage or loan. Attorneys use it to determine the current worth of expected cash flows in legal settlements. Wikinvest defines present value as “today’s value of a set of cash flows that will occur in the future. It is calculated by dividing future cash flows by an appropriate discount rate.” The Ultimate Financial Calculator is designed to calculate present value for any cash flow scenario.

All users should complete the more detailed first tutorial to understand the Ultimate Financial Calculator’s (UFC) basic concepts and settings.

Assume you have won a lottery. The lottery commission offers you two choices: monthly payments of $35,045.00 for 20 years, or a one-time lump-sum payment of $5,476,123.50. Which option is better?

To calculate the present value, follow these steps:

1. Set Schedule Type to “Savings”.
   • Or click the New button to clear any previous entries.
2. Set Rounding to “Open balance—no adjustment”.
   Select Settings > Rounding Options.
3. In the header section, apply the following settings:
   1. Set Calculation Method to “Normal”.
   2. Set Initial Compounding to “Exact/Simple”.
   3. Set Initial Interest Rate to 5.5.
      • This represents your assumed annual investment return. It is also referred to as the discount rate.

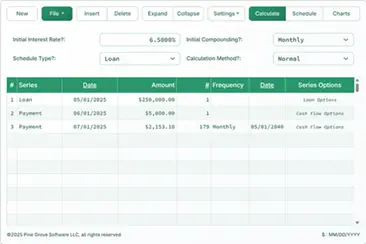
4. In row one of the cash flow input area, create a “Withdrawal” series:
   1. Set the Date to October 3, 2024.
   2. Set the Amount to “Unknown”. Fig. 1
   3. Set # Periods to 1.
      • Note: Because the number of periods is 1, you will not be able to set a frequency.
      • If you attempt to set a frequency, it will be cleared when you exit the row.

5. Create the anticipated series of lottery payments in the second row:
   1. Select “Deposit”.
   2. Enter the Date as November 1, 2024.
      • This is the expected date of the first payment from the lottery commission.
   3. Enter the Amount as $35,045.00 (periodic winnings).
   4. Enter 240 for # Periods.
   5. Select “Monthly” for Frequency. The calculated End Date will be October 1, 2044 (the final payment date).

7. Click the Calculate button.
   • The result is $5,063,030.40. Fig. 2

• • Assuming a future cash flow of 240 monthly deposits of $35,045.00 each, the present value is $5,063,030.40. This is less than the lottery’s lump-sum offer of $5,476,123.50. Therefore, based on value alone, accepting the lump sum appears to be the better option.

Note 1: The cash flow may consist of a single amount or a series of deposits, withdrawals, or payments. You can define multiple series as needed. When calculating present value, the first entry should always be set to “Unknown”, with the Date set to today and the Series set opposite to that of the future cash flow.

Note 2: This example does not account for tax consequences. Taxes can significantly affect the result. Consult a qualified tax professional before making any financial decision.

Note 3: This example also does not account for risk. If you accept the lump sum, are you confident you can invest it to equal the future value of the monthly payments? If you choose the series of payments, is there a risk that the provider might not fulfill the full obligation? If future payments are uncertain, accepting a lower lump sum may be the safer choice.

Back to the Ultimate Financial Calculator.