How to Calculate Future Value
To set your preferred currency and date format, click the “$ : MM/DD/YYYY” link in the lower right corner of any calculator.
A Step-by-Step Tutorial
Tutorial 19
Calculating future value is one of the most common financial tasks.
Wikinvest defines future value as “the amount that an investment made today will grow into at some point in the future.” The Ultimate Financial Calculator can calculate the future value (FV) for any scenario and any cash flow pattern.
Most future value examples involve a series of deposits and answer the question: “What will my savings be worth on a future date?” This tutorial uses a different approach. It begins with a lump sum and applies regular withdrawals to answer: “What will the balance be after making X withdrawals of Y amount?”
The same method can also be used to answer the traditional future value question.
All users should first complete the more detailed first tutorial to understand the Ultimate Financial Calculator’s (UFC) basic concepts and settings.
To calculate the future value of a cash flow, follow these steps:
- Set Schedule Type to Savings.
- Alternatively, click the button to clear any previous entries.
- Click , then select . Set “Rounding” to Adjust last amount to reach “0” balance.
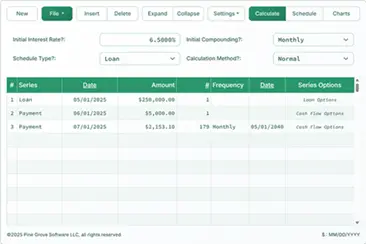
- In the header section, make the following settings:
- For Calculation Method, select Normal.
- Set Initial Compounding to Daily.
- Enter 4.5 for Initial Interest Rate.
- In row 1 of the cash-flow input area, create a Deposit series.
- Set the “Date” to October 1, 2024.
- Set the “Amount” to $50,000.00. This is the starting balance.
- Set the “# Periods” to 1.
- Note: When the number of periods is 1, the frequency setting is disabled. If a frequency is entered, it will be cleared when you leave the row.
- In row 2, create a Withdrawal series.
- Set the “Date” to October 1, 2024.
- Set the “Amount” to $1,000.00.
- Set the “# Periods” to 48.
- Set the “Frequency” to Monthly.
- In row 3, create another Withdrawal series.
- Set the “Date” to September 1.
- This date calculates the future value immediately after the final withdrawal.
- Set the “Amount” to Unknown by typing U.
- Set the “Date” to September 1.

- Click the button.
- The result is $7,225.50.

- To view the detailed cash flow schedule and see how much interest is earned, click the button.
- Total withdrawals: $55,225.49
- The initial deposit earns $5,225.49 in interest while being drawn down.

Note: To calculate a future value, the final row in your schedule must have its amount set to Unknown. You may enter as many deposits or withdrawals as needed—with varying dates, rates, or amounts—but the final cash flow must be an unknown value.
You can automatically increase or decrease withdrawal amounts by clicking and choosing either Amount Step or Percent Step. For example, to apply 2% annual inflation to a monthly withdrawal, set a percent step of 0.1666% (that is, 2.0% divided by 12).
Variations: The Ultimate Financial Calculator can also calculate future value for other scenarios:
Variation 1: To calculate the future value of a series of deposits, use the same setup. In Step 5, change the second event’s series to Deposit, and set the “Date” to November 1, 2024. Instead of withdrawing $1,000 monthly, you will deposit $1,000 monthly, starting one month after the initial deposit. Then, in Step 6, set the “Date” to October 1, 2028 and the “Amount” to Unknown. Click . The new future value is $112,582.05.

Variation 2: To calculate the future value of a single amount, return to the original setup. Click the second input row, then click to remove it. In row 2, set the “Date” to October 1, 2028 and the “Amount” to Unknown. Click . The result is $60,017.52. This means that $50,000 today grows to $60,017.52 in 4 years at 4.5% interest with daily compounding.

Back to the Ultimate Financial Calculator.