IRR Calculator
What is an Internal Rate of Return (IRR) calculation?
This IRR calculator calculates an annualized rate-of-return plus profit (loss).
- Supports dated cash flows
- Easy bulk data entry
- Save entries to a file for later recall
- Know your rate of return across multiple accounts and investments
Answers the question: "How am I doing?"
The Internal Rate of Return (IRR) is the annualized rate of return on an investment. It is calculated from the amounts and dates of the cash flows. It does not require an externally specified interest rate. For this reason, it is called “internal.” This calculator uses the Newton–Raphson method to compute the IRR.
An Internal Rate of Return calculator (IRR) calculates the investment outcome. The results let you compare two or more investment options on a consistent basis.
This calculator determines the IRR for a complex series of cash flows. It also reports the total invested amount, the total returned amount, and the profit (or loss). The calculator supports both irregular time periods and exact date data entry.
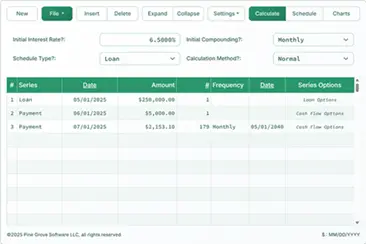
The frequency option defines regular cash flows, such as daily, monthly, or quarterly payments. There are 11 frequency choices.
Review the usage tips below (click to scroll). …
The Calculator-Calculate the Internal-Rate-of-Return for an Irregular Cash Flow
Information
- Jan. 28, 2025: You can now use copy/paste (Ctrl-C/Ctrl-V [Cmd-C on a Mac]) to copy and paste a value from one cell to another cell.
Why is the IRR useful?
The Internal Rate of Return (IRR) converts uneven project cash flows into a single annualized rate of return. Investors can compare opportunities on a comparable basis. Because IRR reflects both the amounts and the timing of cash flows, it standardizes results across investments that have different patterns of outlays and receipts.
For example, consider two rental properties for sale. The asking prices are approximately the same, and the projected rents are approximately the same. One property requires a higher initial renovation cost. The other has higher property taxes. How can an investor determine which purchase is the better investment?
An investor can use an IRR calculator to make this determination.
Caution: Do not compare internal rates of return calculated with different calculators.
Why is this important?
Two different calculators may compute results slightly differently, and neither is necessarily incorrect. (For example, Microsoft Excel includes two IRR functions that may return different results for the same cash flows.) Users do not need to focus on this point, but it is important to be aware of it when interpreting results.
For the record, this calculator determines the IRR using Newton–Raphson method and by counting days (some calculators instead count periods).
To try a calculator that applies a different IRR algorithm, use this site’s Annual Percentage Rate (APR) calculator. The APR calculator follows the method specified in the Truth-in-Lending Act for calculating APR, which is a form of IRR.
Calculator usage and tips
- Zero amounts do not affect the IRR. For example, if the frequency is “Monthly,” and there are only four cash flows in a year, leave the remaining eight at 0. The same applies to 0 amounts after you enter the final liquidation value.
- Enter the investment’s current or final value as the last cash flow. If you are calculating the IRR for a stock or mutual fund and you still own the investment, enter the investment’s current value as the last amount.
- You do not need to enter cash flows in date order. The calculator will sort them before calculating the result. This feature is convenient if you realize that you missed a cash flow. In that case, enter the amount in any available cell, change the date for that cell, and then click
Calcto sort. - If you mistakenly duplicate a cash flow, set one of the duplicates to “0.”
- Changing
First Cash Flow Datewill reset the dates without clearing the values you have entered. - Depending on the order in which you use
First Cash Flow Date,Remove 0’s, andAdd Series, theFirst Cash Flow Datemay not be the first date in the input area. This is not an error. ChangingFirst Cash Flow Dateinitializes a series beginning on the selected date. However, the user can change the date, or the date can be removed withRemove 0’sif the value for the start date is 0. Finally, a user can insert a series with a date that occurs beforeFirst Cash Flow Date. - Calendar Tip: When using the calendar, click the month at the top to list months. If needed, click the year at the top to list years. Click to select a year, then select a month, and then select a day. You can also scroll through the months and days. Or, click
Todayto select the current date. - If you prefer not to use the calendar, single click on a date or use the Tab key (or Shift+Tab) to select a date. Then type eight digits only—there is no need to type the separators. Because the date is already selected, you do not need to clear the prior date before typing. For example, if your selected date format is
mm/dd/yyyy, then for August 1, 2025, type08012025. - Important reminder: You do not need to enter the cash flows in date order. The calculator will sort them once you click the
Calcbutton.
An important reminder about IRR calculators
Different IRR calculators may use different algorithms to determine the rate of return. (There is no single formula for calculating IRR.) Do not compare the results from one IRR calculator for one investment with the results from a different calculator for another investment. Always use the same calculator when comparing multiple investments.
Internal Rate of Return—IRR Equations
Fig. 2—Step-by-step solution of the IRR equation.
Variables: PMT0 = −50,000; PMT1 = −10,000; PMT2 = −12,000; PMT3 = 90,000; n = 3; f = 1.
Variable Definitions
- r
- Periodic rate of return per period. For example, per year when cash flows are annual.
- IRR
- Nominal annualized rate of return, computed as
IRR = r × f. - f
- Frequency (the number of periods per year). For annual spacing,
f = 1. - PMT
- Cash flow at period index
t. By convention, outflows are negative and inflows are positive. Values may differ across periods. - n
- Total number of periods after
t = 0. The summation fromt = 0tot = nincludes both the initial cash flow att = 0and the final cash flow att = n. - t
- Period index. An integer with
t = 0, 1, …, n, measured in equal time steps. (The calculator does not require cash flows to be equally spaced.)
- How do you calculate IRR?
To calculate the Internal Rate of Return (IRR), solve for the interest rate that makes the Net Present Value (NPV) of a series of cash flows equal to zero. Because the IRR equation is nonlinear, it is usually solved using an iterative method such as Newton–Raphson.
Detailed Explanation
The IRR equation is nonlinear and cannot be solved algebraically. To find the rate r that makes NPV equal to zero, treat the problem as a root-finding problem. This requires solving the following equation:
We want r such that f(r) = 0. The Newton–Raphson method is applied for this purpose. It begins with an initial estimate and refines that estimate using both the value and the slope (derivative) of the function at that point.
The slope is the derivative of f(r), denoted f’(r), which shows how sensitive the NPV is to changes in r. It is computed as:
The Newton–Raphson update formula is:
Each iteration produces a value that is closer to the IRR. This process is illustrated in Fig. 2, which shows the calculation using sample cash flows.
Calculation Steps Explained—Fig. 2.
- What is the IRR for the cash flows −50,000 (investment), −10,000, −12,000, +90,000 (returned), each spaced one year apart?
Solve for the periodic IRR by setting the Net Present Value (NPV) to zero, defining
f(r)as the sum of discounted cash flows andf’(r)as its derivative, and then applying Newton–Raphson updates (Equation (6)) untilf(r)converges to zero.- Define the NPV function
f(r)from Equation (2):f(r) = −50,000 − 10,000 ÷ (1 + r)^1 − 12,000 ÷ (1 + r)^2 + 90,000 ÷ (1 + r)^3 - Apply the general derivative rule (Equation (5)) to compute
f’(r):f’(r) = 10,000 ÷ (1 + r)^2 + 24,000 ÷ (1 + r)^3 − 270,000 ÷ (1 + r)^4(Each term follows−t × PMT_t ÷ (1 + r)^(t+1).) - Choose an initial guess for the periodic rate:
r₀ = 0.10. - Compute discount factors at
r₀(first iteration shown in full):(1 + r₀) = 1.10 (1 + r₀)^−1 = 1 ÷ 1.10 ≈ 0.90909091 (1 + r₀)^−2 = 1 ÷ (1.10)^2 ≈ 0.82644628 (1 + r₀)^−3 = 1 ÷ (1.10)^3 ≈ 0.75131480 (1 + r₀)^−4 = 1 ÷ (1.10)^4 ≈ 0.68301346 - Evaluate
f(r₀)using Equation (2):f(r₀) = −50,000 + [−10,000 × 0.90909091] + [−12,000 × 0.82644628] + [90,000 × 0.75131480] ≈ −50,000 − 9,090.90910 − 9,917.35536 + 67,618.33200 ≈ −1,389.93238167Result:
f(r₀) ≈ −1,389.93238167 - Evaluate
f’(r₀)using Equation (5) (term by term):- t = 1, PMT₁ = −10,000:
−1 × (−10,000) ÷ (1 + r₀)^2 = +10,000 × (1 + r₀)^−2 ≈ 10,000 × 0.82644628 - t = 2, PMT₂ = −12,000:
−2 × (−12,000) ÷ (1 + r₀)^3 = +24,000 × (1 + r₀)^−3 ≈ 24,000 × 0.75131480 - t = 3, PMT₃ = +90,000:
−3 × (+90,000) ÷ (1 + r₀)^4 = −270,000 × (1 + r₀)^−4 ≈ −270,000 × 0.68301346
Sum: 10,000×0.82644628 + 24,000×0.75131480 − 270,000×0.68301346 ≈ −158,117.61491701Result:
f’(r₀) ≈ −158,117.61491701 - t = 1, PMT₁ = −10,000:
- Apply the Newton–Raphson update (Equation (6)):
r₁ = r₀ − f(r₀) ÷ f’(r₀) = 0.10 − (−1,389.93238167) ÷ (−158,117.61491701) = 0.10 − 0.00879049676 ≈ 0.09120950 - Discount factors at
r₁(results only):(1 + r₁)^−1 ≈ 0.91641431(1 + r₁)^−2 ≈ 0.83981518(1 + r₁)^−3 ≈ 0.76961865(1 + r₁)^−4 ≈ 0.70528954 - Evaluate at
r₁(results only):f(r₁) ≈ 23.75294757f’(r₁) ≈ −163,559.17595169 - Update (results only):
r₂ = r₁ − f(r₁) ÷ f’(r₁) ≈ 0.09135473 - Discount factors at
r₂(results only):(1 + r₂)^−1 ≈ 0.91629236(1 + r₂)^−2 ≈ 0.83959169(1 + r₂)^−3 ≈ 0.76931145(1 + r₂)^−4 ≈ 0.70491420 - Evaluate at
r₂(results only):f(r₂) ≈ 0.00666170f’(r₂) ≈ −163,467.44351228 - Update (results only):
r₃ = r₂ − f(r₂) ÷ f’(r₂) ≈ 0.09135477 - Discount factors at
r₃(results only):(1 + r₃)^−1 ≈ 0.91629233(1 + r₃)^−2 ≈ 0.83959163(1 + r₃)^−3 ≈ 0.76931136(1 + r₃)^−4 ≈ 0.70491410 - Final convergence (results only):
f(r₃) ≈ 0.00000000f’(r₃) ≈ −163,467.41777956r ≈ r₃ − f(r₃) ÷ f’(r₃) ≈ 0.09135477 - Annualize using frequency
f = 1:IRR = r × f ≈ 0.09135477IRR ≈ 9.135477%
Thus, the periodic IRR is
r ≈ 0.09135477, and with annual spacing (f = 1) the internal rate of return isR ≈ 9.135477%.- Define the NPV function
Notes:
- First iteration shown in full: Discount factors, function values, the derivative, and the update are expanded with explicit arithmetic. Later iterations show results only; they follow the same structure.
f(rₖ)vs.f’(rₖ):f(rₖ)is the NPV at stepk.f’(rₖ)is the slope (derivative) of the NPV with respect torat that step and appears in the denominator of the Newton–Raphson update (Equation (6)).- Stopping criterion: Iteration stops when
|f(rₖ)|is sufficiently close to zero so another update would not materially changer.
Final Answer
The final answer (IRR) is approximately 9.135%.
Validate the calculator. Three-year internal rate of return calculation.
| Initial Investment: | −50,000.00 |
|---|---|
| Initial Investment Date: | |
| First Cash Flow Date: | |
| Cash Flow Frequency: | Annually |
| Discount Rate (optional): | 0.0% |
| No. | Date | Description | Amount |
|---|---|---|---|
| 1 | Additional investment | −10,000.00 | |
| 2 | Additional investment | −12,000.00 | |
| 3 | Investment return | 90,000.00 | |
| If any period includes February 29 (leap year), the result may differ slightly. | |||
Calculated result:
| Internal Rate of Return (IRR): | =9.135% |
|---|
Notes:
- This example uses the same calculation shown in Fig. 2.
- The calculator computes an Extended Internal Rate of Return (equivalent to a spreadsheet’s
XIRRfunction). Extended IRR offers greater flexibility and accuracy because cash flow entries use actual dates. A one-day difference will result in a slightly different (X)IRR.
IRR Calculator Help
The Internal Rate of Return (IRR) is the annualized rate of return on an investment, expressed as a percentage.
An investment can include a series of cash flows. There may be more than one investment (outflow) and more than one withdrawal or return (inflow). However, there must be at least one investment (outflow) and at least one return (inflow). Cash flows may occur on any date and for any amount.
It is essential to use the correct sign (positive or negative) for each cash flow. How do you determine the correct sign?
Consider this rule: When you first invest, you make a payment or transfer funds. A payment decreases your account balance. Therefore, enter all investment cash flows, including the “Initial Investment,” as negative values.
When you receive money from the investment, you deposit it into your account. A deposit increases your account balance. Therefore, enter all investment returns, including the final liquidation value of your investment, as positive values.
The scheduled dates update each time you change the Cash Flow Frequency. The new dates are calculated based on the First Cash Flow Date. However, the Cash Flow Frequency setting does not by itself affect the IRR result. The calculator uses the Cash Flow Frequency only to create dates that match your expected investment cash flows. For example, if you generally make additional investments or withdrawals twice per year, set Cash Flow Frequency to Semiannually.
Comments, suggestions & questions welcomed...