Accurate Future Value Calculator
Introduction to Future Value and the Future Value Calculator
The value of money changes over time. What a dollar buys today is not what it will buy in the future. What the dollar buys in the future is its future value. A future value calculator is a tool that calculates the dollar’s future value.
Two factors affect the dollar’s FV (and any other currency’s FV):
- Inflation (or deflation)
- Investment rate of return
The higher the inflation rate, the less the dollar will buy. The higher the investment rate of return (or interest rate)—or the greater the rate of deflation—the more the dollar will buy.
This future value calculator calculates the FV of an amount or asset after an exact number of days. It supports any rate of return (tested up to 99% per year) for 12 compounding frequencies, plus simple interest.
Because this calculator is date-sensitive and supports multiple compounding options, it is suitable for calculating the balance of a debt if the debtor has made no payments. More details appear below the calculator…
The Calculator-Calculate the Future Value of an Amount
Information
More About Future Value
The future value calculator usually calculates a nominal future value. This means the calculated amount reflects investment gains or interest earned on the money. A nominal future value does not reflect the effect of inflation.
If you want to know the real future value, you can calculate it in one of two ways.
How Does Inflation Affect Future Value?
If you want to know the purchasing power of the original amount after inflation, subtract an estimated inflation rate from the annual interest rate. For example, if your annual interest rate is 4.5% per year and you estimate that inflation will average 2% per year, then instead of entering 4.5% as your rate of return, you would enter 2.5%. The calculated FV will represent the real future value.

This terminology can be misleading. Economists call this the real future value, but it is only an estimated real future value because we can only estimate the future rate of inflation.
However, the real future value is a more accurate measure than the nominal future value, which does not take inflation into account.
If you want to be explicitly compensated for inflation, add the inflation rate to the annual interest rate. For example, if someone owed you $2,000 for 5.5 years and agreed to compensate you for 2% inflation in addition to a 4% interest rate, then you would add the inflation rate to the rate of return.
The result reflects the effect of inflation. Another way to state this is: if an investor wants to earn a real 4.5% gain on an investment, how much must the investor also earn to offset the loss of value from inflation?
The future value calculator makes all of these calculations straightforward.
Future Value Equations
In this section:
Future Value Equation – Daily Compound Interest
Variables: PV = 10,000; R = 10%; d = 365; n = 730.
Variable Definitions
- R
- Nominal annual interest rate.
- d
- Days in a year, typically 360 or 365.
- i
- Daily interest rate.
- PV
- Present value — the principal amount (initial investment).
- n
- Number of days in the term.
Calculation Steps Explained – Fig. 2
- What is the future value of $10,000 invested for two years with daily compounding at a 10% annual interest rate?
To calculate the future value (FV) of an investment with daily compounding, use the formula
FV = PV × (1 + i)n, wherei = R ÷ dandnis the number of days in the term:- Calculate the daily interest rate:
i = 0.10 ÷ 365 ≈ 0.0002739726027…. - Substitute the values into the formula:
FV = 10,000 × (1 + 0.0002739726027…)730. - Simplify the base:
1 + 0.0002739726027… ≈ 1.0002739726027…. - Raise the base to the 730th power:
(1.0002739726027…)730 ≈ 1.22136930164…. - Multiply by the principal:
10,000 × 1.22136930164… ≈ 12,213.69.
The investment grows to $12,213.69 after two years of daily compounding at a 10% annual interest rate.
- Calculate the daily interest rate:
Step-by-step Solution – Fig. 2
i = 0.10 ÷ 365 ≈ 0.0002739726027…FV = 10,000 × (1 + 0.0002739726027…)730≈ 10,000 × (1.0002739726027…)730≈ 10,000 × 1.22136930164…≈ 12,213.69
Final Answer
The final answer (FV) is approximately $12,213.69, of which $2,213.69 is interest (I).
Validate the calculator. Two-year daily compound interest.
| Present Value (PV): | $10,000.00 |
|---|---|
| Annual Interest Rate: | 10.0% |
| Days: | <calculated> |
| Start Date: | |
| End Date: | |
| Compounding Frequency: | Daily |
| Days in a Year: | 365 |
| Future Value (FV): | = $12,213.69 |
| Gain on Investment (Interest Earned): | $2,213.69 |
Notes:
- This example uses the same calculation shown in Fig. 2.
- For daily compounding, the calculator always uses days as the time unit when calculating the term (n).
- You can either enter two dates that are exactly two years apart (the calculator will determine the number of days), or—
- Enter a specific number of days (e.g., 365 or 366 if February 29 is included), and the calculator will determine the end date.
Future Value – Daily Simple Interest
Variables: PV = 10,000; R = 10%; d = 365; n = 730 (two years).
Variable Definitions
- R
- Nominal annual interest rate.
- d
- Number of days in a year (commonly 360 or 365).
- i
- Daily interest rate.
- PV
- Present value — the principal amount (initial investment).
- n
- Number of days in the investment term.
Calculation Steps Explained – Fig. 4
- What is the future value of an investment of $10,000 invested for two years with simple interest at a 10% annual interest rate?
To calculate the future value (FV) of this investment under daily simple interest, use the formula
FV = PV + PV × i × n, wherei = R ÷ dandnis the number of days in the term. The steps are:- Calculate the daily interest rate:
i = 0.10 ÷ 365 ≈ 0.0002739726027…. - Substitute the known values into the formula:
FV = 10,000 + 10,000 × 0.0002739726027… × 730. - Multiply the daily rate by the number of days:
0.0002739726027… × 730 ≈ 0.20000000000000…. - Multiply that result by the principal:
10,000 × 0.20000000000000… ≈ 2,000.00. - Add the interest to the original principal:
10,000 + 2,000.00 ≈ 12,000.00.
The investment grows to $12,000.00 after two years of daily simple interest at a 10% annual interest rate.
- Calculate the daily interest rate:
Step-by-step Solution – Fig. 4
i = 0.10 ÷ 365 ≈ 0.0002739726027…FV = 10,000 + 10,000 × 0.0002739726027… × 730≈ 10,000 + 10,000 × 0.20000000000000…≈ 10,000 + 2,000.00FV ≈ 12,000.00
Final Answer
The final answer (FV) is approximately $12,000.00, of which $2,000.00 is interest.
Validate the calculator. One-year, monthly-compounded interest.
| Present Value (PV): | $10,000.00 |
|---|---|
| Annual Interest Rate: | 10.0% |
| Number of Days: | <calculated> |
| Start Date: | |
| End Date: | |
| Compounding Frequency: | Exact ÷ Simple |
| Days in a Year: | 365 |
| Future Value (FV): | $12,000.00 |
| Total Interest (Gain): | $2,000.00 |
Notes:
- This example uses the same calculation shown in Fig. 4.
- For simple interest, the calculator always measures time in days.
- You can either enter two dates exactly two years apart (the calculator will calculate the number of days), or—
Future Value Calculator Help
This calculator computes the future value (FV) of a single amount. Use the “future value schedule” feature if you want to calculate the future value of a series of investments or deposits.
Enter the present value (the amount invested) and the nominal annual interest rate.
Date Math: If you change either date, the calculator will determine the number of days. If you enter a positive number of days, the end date will update. If you enter a negative number of days, the start date will update.
This feature allows you to calculate FV for a specific number of days without needing to specify calendar dates. For example, if you want the FV after 31 days, enter “31” as the number of days. The specific start and end dates are not important.
Set the compounding method and the number of days in a year. Then click “Calc.” The calculator will display the future value (initial amount plus total interest).
The gain may be calculated based on a fixed unit of time, such as one month. In that case, the monthly gain is always the same for the same annual interest rate and the same principal balance, regardless of the actual length of the month. For example, with a principal of $10,000 and an annual interest rate of 6.75%, the monthly gain for February is the same as the monthly gain for March.
Tips for Entering Dates
To set your preferred currency and date format, click the “$ : MM/DD/YYYY” link in the lower-right corner of any calculator.
You may set a date either by clicking the calendar button [] or by typing 8 digits according to the selected date format.
If you are using the calendar: To quickly change to a new date, click the current month’s name at the top to open a list of months. Then click the year to open a list of years. Select the year, then the month, and finally the date. You can also click “Today” to select the current date.
If you are using the keyboard: Type only the 8 required digits. Do not type separators (“/” or “-”). When you tab to a date input or single-click it, the entire date will be selected. You can begin typing to overwrite it—there is no need to delete it first. Alternatively, press the right arrow key to clear the selection and use backspace to edit. Depending on the selected date format, you can backspace to clear the last two digits of the year and reenter them to change the year quickly.

Greg Mettam says:
Are you able to provide a version of the future value calculator in which the interest rate can be set to monthly as well as yearly?
Karl says:
Of course, nearly anything can done. Do you mean you want to enter a monthly interest rate? And what do you mean by "provide?" Do you want a custom version to install on your own website? Or do you want me to host a calculator with such a feature? If the latter, I would be able to add the feature to this calculator, but I would need to have a good use case for doing so. Mostly, I would think users could convert a monthly rate to an annual rate.
Greg says:
Hi Karl and thanks for your reply.
As a lawyer I do a lot of debt recovery work but I sometimes struggle to find a suitable calculator. If you can host a debt recovery calculator with a full suite of options, that would be very helpful. However, if you don’t want to do that, I am open to the idea of a bespoke calculator for my use only.
Karl says:
hi Greg, by any chance does this debt calculator have what you need?
Greg says:
Karl, I need to calculate the interest due on a specific debt so that I can claim that interest in court proceedings. A debt reduction calculator cannot do that.
Karl says:
I see.
Then this amortization schedule will create a generic, but with dates loan schedule that will accurately show the interest assuming payment were made when they were due.
If you need something less generic, where you can record the payments as they came in, and that will calculate the balance due as of any date (and the interest paid to date), then this calculator is the better choice.
Greg says:
The Ultimate Loan Payoff Calculator is quite helpful but it needs to be changed for debt recovery purposes. For example, all references to a loan and a payment frequency have to removed. Also, I need to claim interest at a monthly rate (if applicable) not just an annual rate. Can this be done?
Karl says:
The C-Value! program, which works like the UFC, allows the user to set the label descriptions (under settings and event names).
Adding the the ability to select interest rates based on a month, would be quite costly. The calculator is complex and to add the feature would take a lot of testing. I’m not inclined to do it because no one (as I recall) has ever asked for the feature. If someone wanted a custom version it could be arrange, but it would be in the 5 figures.
However, as I believe I mentioned before, one could convert a monthly rate to an annual rate. For example, a monthly rate of 1.2% is equal to an annual rate of 14.4% (1.2 x 12). Both values return 488.71 interest on $10,000 for 4 months.
Nate says:
If I had a loan of $100 at 5% and I wanted to compound annually with 360 days in a year, I noticed that at 364 days, gain on investment is $5.06. If you put in 365 days, my gain on investment is down to $5. Why is that?
Karl says:
This is due to the oddities of calendars and interest calculations.
With annual compounding, the interest rate used is the nominal rate, that is 5% or 0.05. Invest the money for 365 days (assuming the time period does not span a leap year) and the money will be invested for one year and the 5% rate is used.
But, invest the money for 364 days, and since that is less than a year, the annual compounding rate is not applicable. 364 days are all odd days, and therefore the daily rate is used. Since you’ve picked a 360 day year, the interest rate used will be 0.05/360.
One more comment. So you know, I generally do not discuss financial equations. That’s not what this site is about. I can’t afford to spend the time, “getting into the weeds.” Therefore, I limit the question I answer to “What calculator do I use?” and “How do I used this calculator or feature”?
Fola says:
Hi great work done,
Can i get a FV calculator with irregular monthly payments but same interest rate.
Karl says:
Thank you. You sure can. Please see this calculator. Scroll down the page and see tutorial #19, future value calculation with complex cash flows.
Md.Imran Hossain says:
How I can use this calculator on my wordpress website?
Karl says:
This particular calculator is not available as a plugin.
Does this plugin work for you? It calculates future value for a regular cash flow.
Endi says:
Hi Karl,
I would like to know how much life insurance cover I need based on:
– Monthly expenses or income
– Inflation rate
– Periode of coverage
Which calculator should I use to calculate sum amount of coverage?
Thank you Karl
Karl says:
Hi Endi, this is a good question. And it’s one that I’ve not spent much time thinking about, and others might have their own opinion. Thus, take this answer with that caveat!
I believe all you need to do is add up the what you want to insure. So, if you want to buy life insurance to insure 20 years of income, and your annual income is $100,000 then buy $2 million dollars insurance.
But what about inflation, you ask?
Here’s the thing. If the insured dies, the beneficiaries will receive the $2 million at the time of death as a lump sum. As long as the proceeds from the policy are invested and the investment earns a return that matches the inflation rate, then you do not need to worry about the impact of inflation. That is, you do not need to buy more than the sum of the income because inflation will erode its purchasing power.
On the other hand, if you think that the money can be invested for more or less than the inflation rate, then you can make an adjustment. In that case, use this present value of an annuity calculator. Using the above example, you would enter for "Regular Cash Flow Amount" the $100,000.
Entering the right "Annual Discount Rate" is the key.
If you think that you can invest the money and earn an average annual rate of return of say 7% and you think over the same period of time, the rate of inflation will be 5% then for the discount rate, you’ll need to enter 2% (the difference between the investment return and the inflation rate). And in that case, you’ll need less than $2 million of insurance.
On the other hand, if you think that inflation is going to be 5%, but your investments will earn only 3.5% then you need to enter -1.5% as the discount rate, Then you’ll see that you’ll need more than $2 million of insurance.
Hope this helps. (And I hope I didn’t miss anything!)
Endi says:
Dear Karl,
Thank you so much for your response. What you describe in your response is one of several ways to provide insurance, I totally agree of you’ve shared.
The other day I saw an Indonesian website (a broker site) which provides two calculators to calculate the insurance need.
Calculator A will calculate insurance need based on monthly expenditures, and Calculator B will calculate insurance need based on monthly income.
Cases solved with those two calculators is like this:
If someone has USD 1,000 monthly expenditures (or monthly income), and plan on insurance coverage for 5 years, with 3% of inflation rate, that person will need xxx amount of insurance cover so his/ her family could survive for 5 years.
*xxx is the calculation result.
Variables which should be entered on the calculator are:
a. Current monthly expenditures/ income: ______
b. Amount of year will be covered by insurance: ______
c. Yearly inflation rate: ______
The result will be the minimum amount insurance needed.
I tried to calculate of the case above using Future Value of Annuity (FVoA), but the calculation result was different!
Using the calculator on the site, calculation result is 63,710
And if I’m using FVoA, the result is 64,647
I assume that maybe the calculator on the site is not using FVoA, and I don’t have any idea what method they’re using to make the calculation.
Giving the situation above, I hope maybe you could help to identify what method of calculation they are using to calculate the minimum total sum insured, so the result would be the same as what calculated on the site.
Thank you Karl.
Karl says:
Thank you for your follow-up.
I’ve not had a chance to look at, let alone study the other calculator, but on this site, the Ultimate Financial Calculator will create a schedule that shows you you do not need to factor inflation into the calculation when buying life insurance.
This assumes that if there is a death, the proceeds are invested at an investment return that is equal to the inflation rate. Take the example I proposed in my prior comment, $100,000 income for 20 years. That’s $2 million in total income. Buy a $2 million policy.
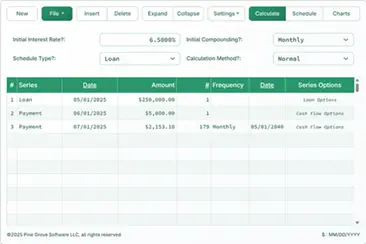
Now, use the UFC calculator to see what happens. Let’s assume a 5% inflation rate. In the calculator, enter:
Initial Interest Rate?: 5.0000%
Initial Compounding?: Annually
Schedule Type?: Savings
Calculate Method?: Normal
In the first row, enter, as a deposit, $2,000,000 and for #period enter 1 i.e. 1 deposit.
In the 2nd row, enter withdraw with the same date as the deposit,
continue in the second row, enter $100,000 and #period 20 and frequency Annually
Now, this is the key, in the rightmost column in the second row, click on "Cash Flow Options," and in the window that opens, select "Percent Step," Starting amount should already show $100,000. Enter 5% as the step amount ("Percent change per level"). That is, you enter your assume inflation rate here. Leave "Number made before change" as 1. Make sure you select Activate “Percent Step” for currently selected series!
Click "Save Changes" to close.
One the main calculator, now click the "Schedule" button. (You can skip the title page options.)
If you look at the schedule, you’ll see that the withdrawals (your income) increase by 5% each year. And at the end of the 20 years, the balance will be very close to 0. Shows you that the $2 million dollar life insurance lasted 20 years and increased by 5 percent each year. This is because the Initial Interest rate (the investment return) equals the step percentage (the income increase each year).
What do you think?
Carlos Castiglia says:
Quiero tener el resultado de una operación en la calculadora de Valor Futuro y no lo consigo: tengo un monto de 8154333, con una Tasa de 30% anual, capitalización mensual en 4 meses de plazo.
Karl says:
¿Por qué no puedes calcular un resultado? La calculadora debería hacerlo automáticamente. Dime los valores que estás ingresando.
Karl says:
Present Value (PV)?: $8,154,333.00
Annual Interest Rate?: 30.0000%
Days (-9,999 # 1969)?: 04/25/2025
End Date (year 2100)?: 08/25/2025
Lo anterior debería funcionar para usted.