Accurate APR Calculator
Introduction to Annual Percentage Rate
The annual percentage rate (APR) is a very important number.
If you are a borrower, it is the one number you should use when you compare loan offers.
If you are a lender in the United States, you must disclose the APR by providing potential borrowers with a Regulation Z APR Disclosure Statement to comply with the law. (See who must prepare a disclosure statement below.)
This calculator will calculate the APR for any closed-end loan and will create a compliant Truth-in-Lending Act disclosure statement.
This article explains what the APR is and why you should use it—not the interest rate—to compare loans. It also explains how to create a disclosure statement.
Let us get started. More below…
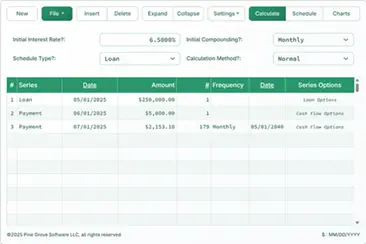
The Calculator-Calculate the APR
Information
What is Annual Percentage Rate or APR?
The Consumer Financial Protection Bureau paraphrases the Truth in Lending Act (TILA) of 1968, which says the “annual percentage rate is the cost of credit expressed as a yearly rate in a percentage.”
What is the difference between an interest rate and the annual percentage rate?
Again, I will paraphrase from the CFPB:
A loan’s interest rate is the cost you pay each year to borrow money, expressed as a percentage. The interest rate does not include fees charged for the loan.
The annual percentage rate is the cost you pay each year to borrow money, including fees, expressed as a percentage. Therefore, the APR is the rate of return earned by the lender.
Rate of return?
Yes—from the lender’s perspective. Remember, the loan is the lender’s investment, and all investors expect to earn a return.
What is important for the borrower to remember is this: the lower the APR, the lower the total cost of the loan. A lower rate of return for the lender means less profit earned on the loan.
Why should a borrower compare APRs and not interest rates?
The APR was created by the TILA to give borrowers a consistent way to compare loans.
Why can I not simply compare the interest rate of two loans and select the loan with the lowest rate?
Here is why.
If you tried to compare loans using only their quoted interest rates, you would need to understand many details about how each loan calculates interest.
For example, you would need to know:
- each loan’s compounding frequency;
- the days-per-year used for odd-day interest calculations;
- the interest allocation method for short or long periods; and
- the impact of fees.
Once you understood these details, you could calculate the interest due and compare the results.
Aside from fees, the APR is not concerned with these details.
Why?
The APR calculation uses the anticipated total payment amounts. Periodic interest is not used in the equation.
Also, the TILA defines rules for how to calculate an APR. All disclosures must use the same equations. This consistency does not apply to interest calculations.
This is why the APR is a very important number.
But the APR is not the only item Regulation Z requires the lender to disclose.
What disclosures does the TILA require?
The federal Truth-in-Lending Act requires that borrowers receive written disclosures about important terms of credit before they are legally bound to pay the loan.
In addition to the APR, the following must be prominently shown:

Finance Charge: the cost of credit expressed as a dollar amount (this is the total amount of interest and certain fees you will pay over the life of the loan if you make every payment when due);
Amount Financed: the dollar amount of credit provided to you;
Total of Payments: the sum of all payments that you will have made at the end of the loan (this includes repayment of principal plus all finance charges).
The TILA disclosure will also include other important loan terms, such as the number of payments, the monthly payment, late fees, whether you can prepay without a penalty, and other conditions. The exact disclosure details depend on the loan itself.
The disclosure statement that this calculator creates is fully compliant with the TILA.
We have defined “APR,” and we have reviewed, at a high level, which terms must be disclosed. How do you use the calculator?
That question is answered in the next section.
Using the APR calculator
The annual percentage rate calculation, as documented in Regulation Z Appendix J, does not depend on many technical details.
The calculation does not need to know the loan’s compounding frequency. It does not matter whether the loan uses 360-day or 365-day years. It does not matter whether the interest is calculated using fixed-length months or the exact number of days in each month.
What the calculation requires is the following:
- The loan amount or amounts.
- The payment schedule, meaning the loan’s principal and interest payment amounts and when they are due. (These payments do not include any charges or fees.)
- The fees or charges the lender requires the borrower to pay.
Using these details, the calculator will calculate the four values lenders must disclose.
- Amount Financed
- Finance Charge
- Annual Percentage Rate
- Total of Payments
The amount financed is calculated by determining the principal loan amount, adding any other financed amounts that are not part of the finance charge, and subtracting any prepaid finance charges such as prepaid interest and loan application fees.
The finance charge is the cost of consumer credit as a dollar amount. It includes any charge payable directly or indirectly by the consumer and imposed as a condition of receiving credit. However, finance charges do not include charges that would also apply in a comparable cash transaction.
Finance charges include, but are not limited to, the following (as quoted from 226.4 of Regulation Z):

- (1) Interest, time price differential, and amounts payable under add-on or discount systems of additional charges.
- (2) Service, transaction, activity, and carrying charges.
- (3) Points, loan fees, assumption fees, finder’s fees, and similar charges.
- (4) Appraisal, investigation, and credit report fees.
- (5) Premiums or other charges for guarantees or insurance that protect the creditor against default.
- (6) Charges paid to another party for purchasing or accepting a consumer obligation when the consumer is required to pay the charge.
- (7) Premiums or charges for credit life, accident, health, or loss-of-income insurance written in connection with credit.
- (8) Premiums or charges for property or liability insurance written in connection with credit.
- (9) Discounts offered to induce payment by a means other than credit.
- (10) Charges or premiums for debt cancellation or suspension coverage written in connection with credit.
Prepaid Interest
Loans can close on any day of the month, not only on a payment due date. If payments are due on the first day of each month and the loan closes on the twenty-sixth, the first payment is often due on the first day of the second month after closing. The period between the closing date and the first payment is longer than one month. This is called a long initial period.
The lender expects interest for the extra days. The interest may be added to the first payment, or it may be collected on the closing date. When collected at closing, it is called prepaid interest.
You can use this interest calculator to calculate exact-day prepaid interest.
In practice, the APR disclosure statement is often an estimate, because it must be provided before the loan closes. The closing date may not yet be known. Therefore, it is usually reasonable to assume regular-length periods.
If the software used to calculate the APR is not accurate, the lender may face fines and reputational risk.
The next section demonstrates the accuracy of this calculator.
All the examples from Regulation Z, Appendix J
Lenders and borrowers need to have confidence in the tools they use.
Is there any better way to prove the accuracy and flexibility of this calculator than to give the user the ability to quickly load each of the 20 calculations from Regulation Z, Appendix J, and allow them to calculate the results?
Of course not.
And that’s just what this page does.
Click on the links below to preload the calculator with the inputs specified by the particular example. You can then click on “Calc” and compare the result with the result defined in the regulation.
Skeptical? Change one of the inputs and recalculate. You’ll see the APR result change.
Not only does this confirm the accuracy of this calculator, but it also shows its flexibility. It handles every closed-end loan examples with multiple loan advances such as construction loans and student loans. (I have not found another calculator on the web that can do these calculations.)
Go ahead, try a few examples. Remember, just click on a link and the details will be preloaded for you in the calculator. No need for manual entry!
The Examples Directly from Regulation Z
Regulation Z classifies the following five examples as “(1) Single advance transaction, with or without an odd first period, and otherwise regular.”
- Example (i): Monthly payment (regular first period)
- Amount advanced = $5,000. Payment = $230.
- Number of payment = 24.
- Loan advance 01/10/1978 First payment 02/10/1978.
- APR = 9.69%
- Example (ii): Monthly payments (long first period)
- Amount advanced = $6,000. Payment = $200.
- Number of payments = 36.
- Loan advance 02/10/1978 First payment 04/01/1978
- APR = 11.82%
- Example (iii): Semimonthly payments (short first period)
- Amount advanced = $5,000. Payment = $219.17.
- Number of payments = 24.
- Loan advance 02/23/1978. First payment 03/01/1978
- Payments made on 1st and 16th of each month.
- APR = 10.34%
- Example (iv): Quarterly payments (long first period)
- Amount advanced = $10,000. Payment = 385.
- Number of payments = 40
- Loan advance = 05/23/1978. First payment = 10/01/1978
- APR = 8.97%
- Example (v): Weekly payments (long first period)
- Amount advanced = $500. Payment = 17.60
- Number of payments = 30.
- Loan advance on 03/20/1978. First payment on 04/21/1978
- APR = 14.96%.
Regulation Z classifies the following two examples as “(2) Single advance transaction, with an odd first payment, with or without and odd first period, and otherwise regular.”

(click on the “example” links to preload each example from TILA)
- Example (i): Monthly payments (regular first period and irregular first payment)
- Amount advanced = $5,000. First payment = $250. Regular payment = $230.
- Number of payments = 24.
- Loan advance on 01/10/1978. First payment on 02/10/1978
- APR = 10.08
- Example (ii): Payments every 4 weeks (long first period and irregular first payment)
- Amount advanced = $400. First payment = $39.50
- Regular payment = $38.31. Number of payments = 12.
- Loan advance on 03/18/1978. First payment on 04/20/1978.
- APR = 28.50%
Regulation Z classifies the following two examples as “(3) Single advance transaction, with an odd final payment, with or without an odd first period, and otherwise regular.”
- Example (i): Monthly payments (regular first period and irregular final payment)
- Amount advanced = $5,000. Regular payment = $230.
- Final payment = $280. Number of payments = 24.
- Loan advance on 01/10/1978. First payment on 02/10/1978
- APR = 10.50%
- Example (ii): Payments every 2 weeks (short first period and irregular final payment)
- Amount advanced = $200. Regular payment = $9.50.
- Final payment = $30. Number of payments = 20.
- Loan advance on 04/03/1978. First payment on 04/11/1978
- APR = 12.22%
Regulation Z classifies the following two examples as “(4) Single advance transaction, with an odd first payment, odd final payment, with or without an odd first period, and otherwise regular.”
- Example (i): Monthly payments (regular first period, irregular first payment, and irregular final payment)
- Amount advanced = $5,000. First payment = $250. Regular payment = $230.
- Final payment = $280. Number of payments = 24.
- Loan advance on 01/10/1978. First payment on 02/10/1978.
- APR = 10.90%
- Example (ii): Payments every two months (short first period, irregular first payment, and irregular final payment)
- Amount advanced = $8,000. First payment = $449.36.
- Regular payment = $465. Final payment = $200. Number of payments = 20.
- Loan advance on 01/10/1978. First payment on 03/01/1978.
- APR = 7.30%
Regulation Z classifies the following four examples as “(5) Single advance, single payment transaction.”
- Example (i): Single advance, single payment (term of less than 1 year, measured in days)
- Amount advanced = $1,000. Payment = 1080.
- Loan advance on 01/03/1978. Payment on 09/15/1978.
- APR = 11.45%
- Example (ii): Single advance, single payment (term of less than 1 year, measured in exact calendar months)
- Amount advanced = $1,000. Payment = $1044.
- Loan advance on 07/15/1978. Payment on 1/15/1979
- APR = 8.80%
- Example (iii): Single advance, single payment (term of more than 1 year but less than 2 years, fraction measured in exact months)
- Amount advanced = $1,000. Payment = $1,135.19.
- Loan advance on 01/17/1978. Payment on 01/17/1980.
- APR = 8.76%
- Example (iv): Single advance, single payment (term of exactly 2 years)
- Amount advanced = $1,000. Payment = $1,240.
- Loan advance on 01/03/1978. Payment on 01/03/1980.
- APR = 11.36%
Regulation Z classifies the following three examples as “(6) Complex single advance transaction.”
- Example (i): Skipped payment loan (payments every 4 weeks)
- Amount advanced = $2135. Payment = $100.
- Number of payments = 24. Payments are due every 4 weeks. However, in those months in which 2 payments would be due, only the first of the 2 payments is made and the following payment is delayed by 2 weeks to place it in the next month.
- Loan advance on 01/25/1978. First payment on 02/20/1978.
- APR = 12.00%
- Example (ii): Skipped payment loan plus single payments
- Amount advanced = $7,350. Loan advance on 03/03/1978
- Payment = $1,000. Number of payments = 3. Payment on 09/15/1978.
- Payment = $2,000. Number of payments = 1. Payment on 03/15/1979.
- Payment = $750. Number of payments = 3. Payment on 09/15/1979.
- Payment = $1,000. Number of payments = 1. Payment on 02/01/1980.
- APR = 10.22%
- Example (iii): Mortgage with varying monthly payments
- Amount advanced (net) = $39,688.56.
- Number of payments = 360.
- Loan advance on 04/10/1978. Payment on 06/01/1978.
- Payments are the same for 12 months at a time.
Regulation Z - 30-year mortgage with varying payments Year Monthly
PaymentYear Monthly
PaymentYear Monthly
Payment1 $291.81 11 $385.76 21 $380.43 2 300.18 12 385.42 22 379.60 3 308.78 13 385.03 23 378.68 4 317.61 14 384.62 24 377.69 5 326.65 15 384.17 25 376.60 6 335.92 16 383.67 26 375.42 7 345.42 17 383.13 27 374.13 8 355.15 18 382.54 28 372.72 9 365.12 19 381.90 29 371.18 10 375.33 20 381.20 30 369.50 - APR = 9.80%
Regulation Z classifies the following two examples as “(7) Multiple advance transactions.”
- Example (i): Construction loan (3 loan advances followed by monthly payments)
- Amount advanced = $20,000 each.
- Loan advances on 04/10/1979, 06/12/1979, and 09/18/1979.
- Payment = $612.36. Number of payments = 240.
- Payment on 12/10/1979.
- APR = 10.25%
- Example (ii): Student loan (8 loan advances, monthly payment, and the first payment before first advance)
- Payment = $240. Number of payments = 50. Payment on 07/01/1978.
- Amount advance = $1,800 on 09/05/78.
- Amount advance = $1,000 on 01/05/79.
- Amount advance = $1,800 on 09/05/79.
- Amount advance = $1,000 on 01/05/80.
- Amount advance = $1,800 on 09/05/80.
- Amount advance = $1,000 on 01/05/81.
- Amount advance = $1,800 on 09/05/81.
- Amount advance = $1,000 on 01/05/82.
- APR = 32.04%
Who must prepare a disclosure statement?
A lender, whether that lender is a business or an individual, must comply with the Truth-in-Lending Act and provide the borrower with a disclosure statement prior to offering or extending credit when four conditions are met:
- The credit is offered or extended to consumers;
- The lender offers or extends credit regularly;
- The credit is subject to a finance charge or is payable by a written agreement in more than four installments; and
- The credit is primarily for personal, family, or household purposes.
Wrapping Up
There is a significant amount to understand about the Truth-in-Lending Act and an APR disclosure statement.
If you are a borrower and you are comparing loan options, compare the APRs. When lenders offer similar quality and similar services, select the loan with the lower APR.

Lisl Unterholzner says:
Your excellent article states: The Consumer Protection Financial Bureau paraphrases the Truth In Lending Act (TILA) of 1968, which says the “annual percentage rate is the cost of credit expressed as a yearly rate in a percentage.”
And the disclosures require the total amount of payments, the total finance charges and the amount financed. There doesn’t seem to be a clear relationship between those three numbers and the APR.
The math in Appendix J looks fairly complicated.
It seems like you should be able to look at the amount of interest you are going to pay and the number of years in relation to the amount financed and get a more straightforward relationship/percentage. Is there something I’m missing about how to interpret APR?
Karl says:
I think that you have the idea, except the unit period is not always the year as you are suggesting. A lot of the complexity comes in when the cash flow is irregular or the amounts change. If you want more details, read about the "Unit Period" in Appendix J.