Accurate APR Calculator
Introduction to Annual Percentage Rate
The annual percentage rate (APR) is a Very Important Number.
If you are a borrower, it is the one number you should use when comparing loan offers.
If you are a lender in the United States, you must disclose the APR by providing potential borrowers with a Regulation Z APR Disclosure Statement in order not to run afoul of the law. (See who must prepare a disclosure statement below.)
This calculator will calculate the APR for any closed-end loan as well as create a compliant Truth-in-Lending Act disclosure statement.
This post discusses what the APR is and why you should use it and not the interest rates to compare loans. I'll also instruct users on how to create a disclosure statement.
Let's get started. More below…
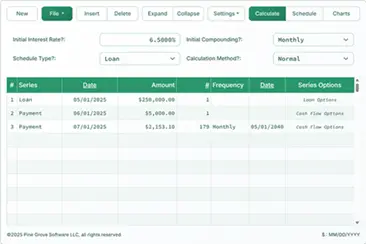
The Calculator-Calculate the APR
Information
What is Annual Percentage Rate or APR?
The Consumer Protection Financial Bureau paraphrases the Truth In Lending Act (TILA) of 1968, which says the "annual percentage rate is the cost of credit expressed as a yearly rate in a percentage."
What is the difference between an interest rate and the annual percentage rate?
Again, I'll paraphrase from the CPFB:
A loan's interest rate is the cost you pay each year to borrow money expressed as a percentage. The interest rate does not include fees charged for the loan.
The annual percentage rate is the cost you pay each year to borrow money, including fees, expressed as a percentage. Therefore, the APR is (basically) the rate-of-return earned by the lender.
Rate-of-return?
Yes! From the lender's perspective. Remember, the loan is the lender's investment and all investor's hope to make a return.
What's important for the borrower to remember, is the lower the APR, the less the loan will cost, which makes sense. The lower the rate-of-return for the lender, the less profit they are earning on the loan they issue.
Why should a borrower compare APRs and not interest rates?
The APR was created by the TILA to give borrowers a way to compare loans.
Why can't I just compare the interest rate of two loans and select the loan with the lowest rate?
Good question, and here's why.
If you wanted to compare two loans using their quoted interest rates, you would have to know and understand a lot of details about how the interest rate is used to calculate each loan's interest.
For example, you would have to know:
- each loan's compounding frequency;
- the days-per-year used for odd day interest calculations;
- the interest allocation method for short or long periods; and
- the impact of fees
Once you understand these details, then you would be able to calculate the interest due and compare the results.
Aside from fees, the APR isn't concerned with these details.
Why?
The APR calculation uses for input the anticipated total payment amounts. Periodic interest never is used in the equation.
Also, the TILA creates rules for how to calculate an APR. All disclosures have to use the same equations. This is not true for interest calculations.
This is why the APR is a Very Important Number.
But the APR is not the only thing that Regulation Z requires the lender to disclose.
What disclosures does the TILA require?
The federal Truth-in-Lending Act requires that borrowers receive written disclosures about important terms of credit before they are legally bound to pay the loan.
In addition to the APR, the following must be prominently shown:

Finance Charge: cost of credit expressed as a dollar amount (this is the total amount of interest and certain fees you will pay over the life of the loan if you make every payment when due);
Amount Financed: the dollar amount of credit provided to you;
Total of Payments: the sum of all the payments that you will have made at the end of the loan (this includes repayment of the principal amount of the loan plus all of the finance charges)
The TILA disclosure will also include other important terms of the loan such as the number of payments, the monthly payment, late fees, whether you can prepay your loan without a penalty, and other important conditions. Exactly what must be included on the disclosure statement varies depending on the conditions of the loan itself.
The disclosure statement that this calculator creates is fully compliant with the TILA.
Alright, we've defined "APR," and we've covered at a high level what loan terms must be disclosed, but how do I use the calculator?
That question gets answered in the next section.
Using the APR calculator
The annual percentage rate calculation, as Regulation Z documents it in Appendix J, does not care about pesky details.
The calculation does not need to know what the loan's compounding frequency is. It does not care if the loan uses 360 or 365 day years. It does not care if the interest is calculated using the same day months or calculated using the exact number of days in a month.
What the calculation requires is the following:
- The loan amount or amounts
- The payment schedule, meaning the loan's principal and interest payment amounts and when they are due. (These loan payments do NOT include any charges or fees.)
- The fees or charges the lender requires the borrower to pay.
Using these details, the calculator will calculate the four values lenders must reveal.
- Amount Financed
- Finance Charge
- Annual Percentage Rate
- Total of Payments
The amount financed is calculated by determining the principal loan amount and adding any other amounts that are financed by the creditor and are not part of the finance charge, and subtracting any prepaid finance charges such as prepaid interest and loan application fees.
The finance charge is the cost of consumer credit as a dollar amount. It includes any charge payable directly or indirectly by the consumer and imposed directly or indirectly by the creditor as an incident to or a condition of the extension of credit. Note, however, finance charges do not include any charge of a type payable in a comparable cash transaction.
Finance charges include but are not limited to the following (as quoted from 226.4 of Reg. Z):

- (1) Interest, time price differential, and any amount payable under an add-on or discount system of additional charges.
- (2) Service, transaction, activity, and carrying charges, including any charge imposed on a checking or other transaction account to the extent that the charge exceeds the charge for a similar account without a credit feature.
- (3) Points, loan fees, assumption fees, finder’s fees, and similar charges.
- (4) Appraisal, investigation, and credit report fees.
- (5) Premiums or other charges for any guarantee or insurance protecting the creditor against the consumer’s default or other credit loss.
- (6) Charges imposed on a creditor by another person for purchasing or accepting a consumer’s obligation, if the consumer is required to pay the charges in cash, as an addition to the obligation, or as a deduction from the proceeds of the obligation.
- (7) Premiums or other charges for credit life, accident, health, or loss-of-income insurance, written in connection with a credit transaction.
- (8) Premiums or other charges for insurance against loss of or damage to property, or against liability arising out of the ownership or use of property, written in connection with a credit transaction.
- (9) Discounts for the purpose of inducing payment by a means other than the use of credit.
- (10) Charges or premiums paid for debt cancellation or debt suspension coverage written in connection with a credit transaction, whether or not the coverage is insurance under applicable law.
Prepaid Interest
A special note about prepaid interest. Loans can and will close on any day of the month, not just on a payment due date. If payments are due on the first and a loan closes (loan amount is made available) on the twenty-sixth, the first payment frequently will not be due until the first of the 2nd month following the closing. That is, if the loan closes on July 26 the first payment will be due on September 1. The time between the loan closing and the first payment is longer than a month. This is called a long initial period. The lender is going to want the interest they are entitled to for these 6 days (July 26 - August 1). They can collect the interest for the 6 days by adding it to the September 1 payment. Or, they can ask for the interest on the day the loan closes. If they collect it on the day the loan closes, this is prepaid interest.
You can use this interest calculator to calculate exact day prepaid interest.
But here's a tip. When it's all said and done, an APR disclosure statement is almost always just an estimate since it has to be given to the borrower even prior to the loan closing. Frequently the closing date isn't even known when the disclosure is provided. Therefore, keep it simple, and just assume regular length periods!
But with that said...
If the software used to calculate the APR is not accurate, the lender may be subject to fines and adverse publicity leading to reputational damage.
The next section will prove to you the accuracy of this calculator.
All the example from Regulation Z, Appendix J
Lenders and borrowers need to have confidence in the tools they use.
Is there any better way to prove the accuracy and flexibility of this calculator than to give the user the ability to quickly load each of the 20 calculations from Regulation Z, Appendix J, and allow them to calculate the results?
Of course not.
And that's just what this page does.
Click on the links below to preload the calculator with the inputs specified by the particular example. You can then click on "Calc" and compare the result with the result defined in the regulation.
Skeptical? Change one of the inputs and recalculate. You'll see the APR result change.
Not only does this confirm the accuracy of this calculator, but it also shows its flexibility. It handles every closed-end loan examples with multiple loan advances such as construction loans and student loans. (I have not found another calculator on the web that can do these calculations.)
Go ahead, try a few examples. Remember, just click on a link and the details will be preloaded for you in the calculator. No need for manual entry!
The Examples Directly from Regulation Z
Regulation Z classifies the following five examples as "(1) Single advance transaction, with or without an odd first period, and otherwise regular."
- Example (i): Monthly payment (regular first period)
- Amount advanced = $5,000. Payment = $230.
- Number of payment = 24.
- Loan advance 01/10/1978 First payment 02/10/1978.
- APR = 9.69%
- Example (ii): Monthly payments (long first period)
- Amount advanced = $6,000. Payment = $200.
- Number of payments = 36.
- Loan advance 02/10/1978 First payment 04/01/1978
- APR = 11.82%
- Example (iii): Semimonthly payments (short first period)
- Amount advanced = $5,000. Payment = $219.17.
- Number of payments = 24.
- Loan advance 02/23/1978. First payment 03/01/1978
- Payments made on 1st and 16th of each month.
- APR = 10.34%
- Example (iv): Quarterly payments (long first period)
- Amount advanced = $10,000. Payment = 385.
- Number of payments = 40
- Loan advance = 05/23/1978. First payment = 10/01/1978
- APR = 8.97%
- Example (v): Weekly payments (long first period)
- Amount advanced = $500. Payment = 17.60
- Number of payments = 30.
- Loan advance on 03/20/1978. First payment on 04/21/1978
- APR = 14.96%.
Regulation Z classifies the following two examples as "(2) Single advance transaction, with an odd first payment, with or without and odd first period, and otherwise regular."

(click on the "example" links to preload each example from TILA)
- Example (i): Monthly payments (regular first period and irregular first payment)
- Amount advanced = $5,000. First payment = $250. Regular payment = $230.
- Number of payments = 24.
- Loan advance on 01/10/1978. First payment on 02/10/1978
- APR = 10.08
- Example (ii): Payments every 4 weeks (long first period and irregular first payment)
- Amount advanced = $400. First payment = $39.50
- Regular payment = $38.31. Number of payments = 12.
- Loan advance on 03/18/1978. First payment on 04/20/1978.
- APR = 28.50%
Regulation Z classifies the following two examples as "(3) Single advance transaction, with an odd final payment, with or without an odd first period, and otherwise regular."
- Example (i): Monthly payments (regular first period and irregular final payment)
- Amount advanced = $5,000. Regular payment = $230.
- Final payment = $280. Number of payments = 24.
- Loan advance on 01/10/1978. First payment on 02/10/1978
- APR = 10.50%
- Example (ii): Payments every 2 weeks (short first period and irregular final payment)
- Amount advanced = $200. Regular payment = $9.50.
- Final payment = $30. Number of payments = 20.
- Loan advance on 04/03/1978. First payment on 04/11/1978
- APR = 12.22%
Regulation Z classifies the following two examples as "(4) Single advance transaction, with an odd first payment, odd final payment, with or without an odd first period, and otherwise regular."
- Example (i): Monthly payments (regular first period, irregular first payment, and irregular final payment)
- Amount advanced = $5,000. First payment = $250. Regular payment = $230.
- Final payment = $280. Number of payments = 24.
- Loan advance on 01/10/1978. First payment on 02/10/1978.
- APR = 10.90%
- Example (ii): Payments every two months (short first period, irregular first payment, and irregular final payment)
- Amount advanced = $8,000. First payment = $449.36.
- Regular payment = $465. Final payment = $200. Number of payments = 20.
- Loan advance on 01/10/1978. First payment on 03/01/1978.
- APR = 7.30%
Regulation Z classifies the following four examples as "(5) Single advance, single payment transaction."
- Example (i): Single advance, single payment (term of less than 1 year, measured in days)
- Amount advanced = $1,000. Payment = 1080.
- Loan advance on 01/03/1978. Payment on 09/15/1978.
- APR = 11.45%
- Example (ii): Single advance, single payment (term of less than 1 year, measured in exact calendar months)
- Amount advanced = $1,000. Payment = $1044.
- Loan advance on 07/15/1978. Payment on 1/15/1979
- APR = 8.80%
- Example (iii): Single advance, single payment (term of more than 1 year but less than 2 years, fraction measured in exact months)
- Amount advanced = $1,000. Payment = $1,135.19.
- Loan advance on 01/17/1978. Payment on 01/17/1980.
- APR = 8.76%
- Example (iv): Single advance, single payment (term of exactly 2 years)
- Amount advanced = $1,000. Payment = $1,240.
- Loan advance on 01/03/1978. Payment on 01/03/1980.
- APR = 11.36%
Regulation Z classifies the following three examples as "(6) Complex single advance transaction."
- Example (i): Skipped payment loan (payments every 4 weeks)
- Amount advanced = $2135. Payment = $100.
- Number of payments = 24. Payments are due every 4 weeks. However, in those months in which 2 payments would be due, only the first of the 2 payments is made and the following payment is delayed by 2 weeks to place it in the next month.
- Loan advance on 01/25/1978. First payment on 02/20/1978.
- APR = 12.00%
- Example (ii): Skipped payment loan plus single payments
- Amount advanced = $7,350. Loan advance on 03/03/1978
- Payment = $1,000. Number of payments = 3. Payment on 09/15/1978.
- Payment = $2,000. Number of payments = 1. Payment on 03/15/1979.
- Payment = $750. Number of payments = 3. Payment on 09/15/1979.
- Payment = $1,000. Number of payments = 1. Payment on 02/01/1980.
- APR = 10.22%
- Example (iii): Mortgage with varying monthly payments
- Amount advanced (net) = $39.688.56.
- Number of payments = 360.
- Loan advance on 04/10/1978. Payment on 06/01/1978.
- Payments are the same for 12 months at a time.
Regulation Z - 30-year mortgage with varying payments Year Monthly
PaymentYear Monthly
PaymentYear Monthly
Payment1 $291.81 11 $385.76 21 $380.43 2 300.18 12 385.42 22 379.60 3 308.78 13 385.03 23 378.68 4 317.61 14 384.62 24 377.69 5 326.65 15 384.17 25 376.60 6 335.92 16 383.67 26 375.42 7 345.42 17 383.13 27 374.13 8 355.15 18 382.54 28 372.72 9 365.12 19 381.90 29 371.18 10 375.33 20 381.20 30 369.50 - APR = 9.80%
Regulation Z classifies the following two examples as "(7) Multiple advance transactions."
- Example (i): Construction loan (3 loan advances followed by monthly payments)
- Amount advanced = $20,000 each.
- Loan advances on 04/10/1979, 06/12/1979, and 09/18/1979.
- Payment = $612.36. Number of payments = 240.
- Payment on 12/10/1979.
- APR = 10.25%
- Example (ii): Student loan (8 loan advances, monthly payment, and the first payment before first advance)
- Payment = $240. Number of payments = 50. Payment on 07/01/1978.
- Amount advance = $1,800 on 09/05/78.
- Amount advance = $1,000 on 01/05/79.
- Amount advance = $1,800 on 09/05/79.
- Amount advance = $1,000 on 01/05/80.
- Amount advance = $1,800 on 09/05/80.
- Amount advance = $1,000 on 01/05/81.
- Amount advance = $1,800 on 09/05/81.
- Amount advance = $1,000 on 01/05/82.
- APR = 32.04%
Who must prepare a disclosure statement?
A lender, whether that lender is a business or an individual must comply with the Truth-in-Lending-Act and provide the borrower with a disclosure statement prior to offering or extending credit when four conditions are met:
- The credit is offered or extended to consumers;
- The lender offers or extends credit regularly;
- The credit is subject to a finance charge or is payable by a written agreement in more than four installments; and
- The credit is primarily for personal, family, or household purposes.
Wrapping Up
As you can see, there is a lot to understanding the Truth-In-Lending Act and an APR Disclosure Statement.
However, if you are a borrower, and you are comparing loan options, just compare the APRs. And assuming the lenders are of similar quality and offer the same or similar services, go with the loan that has the lower APR.

Norman T Roberts says:
How do you calculate APR for an interest only loan with points
Karl says:
I assume you see where to enter the points.
In the grid area of the calculator, you’ll have to create at least 3 rows. 1 loan amount row. I row showing the interest only payment amounts, and a third row for the payoff amount. If the payment amount changes at any point before the final payoff amount, then you would need to add additional rows anytime the payment changes.
The APR does not care about interest only per se. The APR calculation only cares about what the consumer pays.
If this isn’t clear, feel free to ask again.
sherry says:
Do you have a calculator for construction to permanent ARM mortgages where the payments were interest only in year 1?
Karl says:
This calculator will handle construction loans, ARMs and it supports interest-only payments, in the first year, or for any year along with the regular principal and interest payments.
Scroll down the page for tutorials.
Please ask if you have any questions.
Vik says:
I am using example 8. Example (i): Monthly payments (regular first period and irregular final payment).
Is it possible to recreate the calculation in Excel? If so, what wold the formula look like?
Thank you!
Karl says:
There are two questions here. I don’t know Excel programming, so I can’t answer your question if you can recreate it in Excel. As to the formula, get a hold of a copy of the Truth-in-Lending Act (I think I have a link to on the page as I recall). The math is included in the Reg.
Russ Tolleson says:
I am looking for a calculator that will handle ARM loans by accomplishing the following calculations:
Handle a fixed interest period before becoming adjustable (such as a 5/1 or 5/6).
Be able to recalculate the new interest rate and monthly payment at the end of the fixed period and at each rate change period based on the assumption the maximum interest rate change allowed (based on starting rate, margin, caps) at that change period.
Continue the calculation until the maximum interest rate is reached and then amortize out the loan.
Karl says:
My mistake in the last reply. I thought your comment was on a different calculator page.
Please see this adjustable rate calculator page.
It will create an amortization schedule that lets the user change the rate to any interest rate between -99% and 99% on any date. But the user needs to know the rules as to when the rate can change and what the maximum rate is.
ravik sonagra says:
Hi how to download APR calculator plugin
Karl says:
I do not have an APR calculator plugin.
Greg says:
Hi,
Is this calculator available to download/integrate with other software?
I’ve been trying my best to reproduce this type of calculator based on the criteria from section Z, but I’ll be damned if the math is working out.
Karl says:
Hi Greg, yeah, it’s a tough one, isn’t it? I’ll reply to you via email later today or early tomorrow.
Greg says:
Thank you in advance!
Holly Eaton says:
Help. I am a clinical professor in a law school clinic that assists low-income individuals in debt collection cases. In one case I am handling at the moment, I believe the lender has violated the Truth in Lending Act. When I use your online Regulation Z calculator I get an APR that is significantly higher than the stated APR of the loan. That would be a violation of TILA. However, I am unable to duplicate the results I get on your calculator when I use other online calculators. Why is there a discrepancy? Can you help me understand this? How can I prove that yours is right and the others are wrong?
Karl says:
The details are important of course, but I know the one on this site to be very accurate. How do I know that? When developing the calculator, I personally took every APR example in the TILA Act’s Appendix J and plugged the values into the calculator. If you want to do that, you’ll get the exact same results as you find in Reg. Z. I doubt if there are any other online calculators that even are able to support the ability to enter the examples (due to irregular cash flow in the examples for one reason) let alone, calculate the examples.
But, if you want to post the details here (no personally identifiable information of course) and give me a link to another calculator or two, I might be able to give you specific details as to why this one is right.
Holly Eaton says:
The origination date of the loan is 12/13/2016. The stated APR is 15.7% The amount financed is $2,000 over two years. There are no additional fees. The payment amount is listed as 23 payments of $97.47 monthly beginning 01/04/2017 and ending with a payment of $97.35 on 12/04/2018. The total finance charge is $339.16. When that information is plugged into your calculator, the APR comes back as 15.87% which would be a violation of TILA, however, I am unable to generate an amortization schedule that matches these results, including on your website.
Other online calculators do not allow me to adjust the amount of the last payment. When I plug in $97.47 as the monthly amount using the dates listed above, I get an APR of 15.52% which is significantly less than the stated APR of 15.7%.
https://www.calculator.net/apr-calculator.html
https://www.calculatorsoup.com/calculators/financial/apr-calculator.php
Any insight you could provide would be deeply appreciated.
Karl says:
Thank you for the details. I believe I can tell you exactly what is happening, without even looking at the other calculator.
Actual dates are important. A day paid one way or the other does impact the APR.
The good news is, when I enter the number you provided, I get the exact same result with this calculator as you said, i.e. 15.87%, with a calculated finance charge of $339.16. that should confirm neither of us has a data entry error.
My guess is that calculator soup does not allow you to input dates (I think I looked at theirs sometime last year, and that’s what I recall). If you can’t input dates, and you can’t input an accurate last payment, you’ll get inaccurate results. And you can prove it with this calculator.
If a calculator does not ask for dates, it is assuming all periods are of equal length. You example has a loan with a shorter first period, otherwise, the payments would start on Jan. 13, 2017, not Jan. 4. 2017.
Enter into this calculator in the first row, a loan for $2,000 on Dec. 4th, and 24 equal payments of $97.47 (not a final payment of $97.35) and you’ll get 15.52% as the APR, which matches the other calculator.
How’s that? 🙂
As to the amortization schedule, I played around, and I got very close in creating one. The problem I’m having is, you didn’t give me the quoted interest rate. I think that will help if you want to send that over. (But I’ll look tomorrow).
Holly Eaton says:
Thank you so much! This is very helpful.
The loan documents only list the APR, they do not list the interest rate. I was hoping I could find an amortization schedule that allowed me to input the APR and the payment dates and amounts and it would calculate the interest rate then generate an amortization schedule.
If you could point me to an amortization schedule that coincides with the APR generated by your calculator, I would be most appreciative.
Karl says:
You can use this amortization schedule calculator. It will create a printable schedule for you.
The first thing you’ll want to do is go to "Settings" and click on "Long/Short Period Options" Select "No payment reduction"
Enter your loan details including the dates. You should use 15.8736% for the annual interest rate (I backed into that number). Leave payment and compounding frequency set to monthly.
Click on either "Calc" or "Print Preview."
Make sure you’ve entered values in the 4 items at the top of the calculator since there are no unknown attributes to this loan. You can’t have the calculator calculate the interest rate and get the schedule you need. If the calculator calculates a rate, it will calculate a rate that is more accurate, thus eliminating the odd last payment amount. If you fill in the values, you should have a schedule this is off by one penny.
Holly Eaton says:
Perfect! I can’t thank you enough!
Karl says:
You’re welcome! Please send your students to this site, and i would be very curious to hear what happens with the difference in the APR. Will the lender be in hot water? Curious minds want to know!
Holly R Eaton says:
The lender will have to pay double the fees charged, court costs and attorneys fees to defend against the collection action if I can provide an expert who can show that your calculations are correct. Would you be our expert? I reached out to you through LinkedIn. Let me know how to reach you directly.
Karl says:
I did reply to your LinkedIn message, but the best way to reach me is via the email address on the contact page of this site. A link to that page is at the bottom of all pages.
Miguel Cruz says:
Is there a way to get the math to covert into PHP code?
Karl says:
Are you asking if the source code can be ported to PHP, and is it for sale?
Anything is possible. Please get in touch with me via the email address on the contact page.
Miguel Cruz says:
just reply via email. Thank you look forward to your feedback.