Time Value of Money Calculator

Time value of money (TVM) calculator with selectable dates and printable TVM schedules. Solve for one of 5 unknowns:

• Present value - PV
• Term - number of cash flows
• Rate
• Cash flow amount (debit/credit)
• Future Value - FV

Click to Try It Now!

Time Value of Money (TVM) is the concept that the value of money itself changes over time. Having a dollar today is worth more than a dollar tomorrow.

What are the five primary time value of money (TVM) calculations?

• present value (PV)
• future value (FV)
• annuity or cash flow amount
• discount or interest rate
• term or number of periods

This free TVM calculator can perform all these calculations with ease. Just enter a zero for the unknown value.

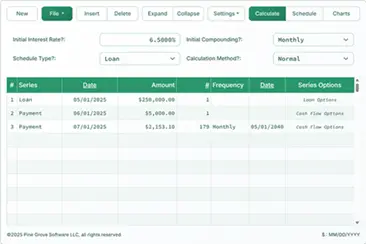
In addition to calculating any of the five possible unknowns, this calculator also creates a time value of money schedule. A TVM schedule is a report which shows the intermittent interest calculations and the arithmetic behind the change from present value to future value. More details below

Time Value of Money Cash Flow (optional)

To Quickly
Pick a Date

The change in value from PV to FV can result from accrued interest being added or deducted from the present value.

Or it can be the result of adding or deducting an additional amount plus the accrued interest to/from the present value.

If there is an additional amount, the additional amount is known as an annuity. Annuity is the financial term for the cash flow. If the amount is added to the PV, then the cash flow is a credit annuity. If it is deducted from the PV, then the cash flow is a debit cash flow.

Having a cash flow is optional.

A loan is a debit annuity TVM calculation. The FV (or loan balance) should be less than the PV at the end of the cash flow term.

A 401 retirement account is a credit annuity TVM calculation. The FV (or account balance) should be greater than the PV at the end of the cash flow term.

TVM Calculator Usage Notes

• If you select "add to PV" for cash flow type, the PV can always be 0, and if you set another input to 0, the calculator will calculate the value of the second input. This allows you to solve for an input value and start with a 0 present value.
• If you select "deduct from PV" for cash flow type, the FV can always be 0, and if you set another input to 0, the calculator will calculate the value of the second input. This allows you to solve for the input value to arrive at a 0 future value.
• The interest rate can be negative. A negative interest rate inverses the usual results.
• If you did not indicate a value to calculate by entering a 0, the calculator will recalculate the PV when the cash flow is deducted from PV, or
• If there is nothing to calculate, the calculator will recalculate the FV when the cash flow is added to the PV