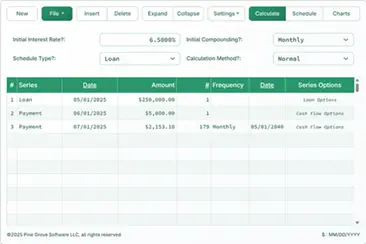
Loan Calculator
How to Use the Loan Calculator
Use this calculator to compute a loan payment.
- Click
Clear, then enter values for:Loan AmountNumber of Payments(term)Annual Interest Rate
- Optionally, set the start date and end date.
- Leave
Loan Payment Amountset to0. - Click
“Calc”or“Payment Schedule”.
Leave the other settings unchanged unless you need to modify them.
This loan calculator also offers many features beyond basic payment calculations. See more below…
The Calculator-Calculate Loan Amount, Rate, Term or Payment Amont
To set your preferred currency and date format, click the “$ : MM/DD/YYYY” link in the lower right corner of any calculator.
Information
Operating Details
Always enter 0 for the unknown value (and reenter 0 after changes).
Note - You must enter 0 for the value you want the calculator to compute.
Why does the calculator not automatically recalculate the last unknown value?
The calculator is designed to generate a payment schedule that matches the loan terms you specify. This behavior is intentional. There is no single “correct” loan payment amount—the payment is valid as long as both the lender and the borrower agree to it. If the calculator always recalculated the last unknown, that flexibility would not be possible.
About the loan origination date (start date) and the first payment due date.
Important - The first loan payment period is rarely equal in length to the regular payment frequency. For example, if the schedule is monthly, the time from loan origination (when the borrower receives the funds) to the first payment due date is usually not exactly one month. The first period is often either longer or shorter.
A longer or shorter first period directly affects the interest calculation.
Very few online calculators handle this detail correctly. For accurate interest and payment results, you must be able to set the loan origination date and the first payment due date independently. You can do this on the Options tab.
Warning - Selecting dates may produce payment amounts and interest charges that do not match the results from other calculators.
This difference is intentional.
If you want results that match other calculators, set the Loan Date and First Payment Due so that the time between them equals one full payment period as defined in Payment Frequency. Example: If the Loan Date is May 15 and the Payment Frequency is Monthly, then set the First Payment Due to June 15. This will produce a conventional interest calculation.
See Long Period Options and Short Period Options below for additional details about payment amounts and interest calculations.
Keeping it simple - If you only need estimates and not precise accuracy, you can leave the dates as they are when the calculator loads.
Much More Than a Payment Calculator
The four required values
Loan Amount— the principal borrowed, not including interest.Number of Payments(term) — thePayment Frequencydetermines the loan term. For a five-year loan with monthly payments, enter60for the number of payments (60 months = 5 years).Annual Interest Rate— the nominal annual interest rate. (If a lender quotes anything other than an annual rate, consider avoiding the loan.)Payment Amount— the amount due on each payment date.
Set one of the above values to 0 if it is unknown.
How much can I borrow?
- Set the loan amount to
0. - Enter the number of payments.
- Enter the annual interest rate.
- Enter the desired or expected payment amount.
- Click
Calc.
How long will it take to pay off a loan?
- Enter the loan amount.
- Set the number of payments to
0. - Enter the annual interest rate.
- Enter the desired or expected payment amount.
- Click
Calc.
What interest rate allows me to pay $350 per month?
- Enter the loan amount.
- Enter the number of payments.
- Set the annual interest rate to
0. - Enter
$350for the payment amount. - Click
Calc.
Three loan options you usually do not need to change
Payment Frequency— how often payments are scheduled. The calculator supports 11 options, including biweekly (every two weeks), monthly, and annually. Payment due dates are calculated from the first payment date.Compounding— in most cases, set the compounding frequency equal to the payment frequency. This produces periodic interest. SelectingExact/Simpleresults in exact-day simple interest.Amortization Method— leave this set toNormalunless you have a specific reason to change it. For a full explanation of available methods, see Nine Loan Amortization Methods.
Results — Loan Summary

See the payment schedule for the total interest saved.
Total Interest— total interest paid over the loan term, assuming payments are made as scheduled.Total Prepaid Principal— the sum of all extra payments. The payment schedule also reports the interest saved.Total Principal & Interest— the loan amount plus interest. This is the total cost of the loan.
Eleven advanced loan options
Loan Date— the date funds are disbursed. For vehicle or home loans, this is the closing date.First Payment Due— for leases, this may be the same as the loan date. See “About the loan origination date (start date) and the first payment due date” above.Extra Payment Amount— enter the amount if you plan to make one or more extra payments.Extra Payments Start— enter the date when extra payments should begin. This does not have to match payment due dates. For example, if regular payments are due on the 1st, you could schedule extra payments on the 15th to align with your pay periods.Extra Payment Frequency— how often you plan to make extra payments. For example, annually when receiving a year-end bonus.Number of Extra Payments— enter any whole number. To continue extra payments until the loan is paid off, enterUfor “Unknown.”Days Per Year— choose 360 or 365. Also called the day-count convention, this affects interest calculations when compounding is based on days (daily, exact/simple, or continuous) or when an initial irregular period creates odd days.Rounding Options— because payment and interest amounts are rounded each period (e.g., 345.0457 becomes 345.05), most loan schedules require a final rounding adjustment to bring the balance to zero. The payment schedule includes a footnote showing the rounding amount.Long Period Options(odd-day interest) — controls how interest is shown when the first period is longer than the selected payment frequency.Short Period Options— controls how payments are adjusted when the first period is shorter than the selected payment frequency.Fiscal Year-End— defines the fiscal year for reporting totals. Use this if your fiscal year does not match the calendar year.
More details about odd-day and irregular-period interest settings

Loan Equations
This section documents the formulas used by the calculator and shows the step-by-step process for solving them. Use the links below to go directly to a specific equation:
- Term equation
- Loan amount equation
- Annual interest rate equation
- Payment amount equation
- Amortization equation
Term Equation — Calculate the Number of Payments (N)
Fig. 2 – Step-by-step solution of the term equation.
Variables: A = 50,000; R = 6 %; P = 1,000; n = 12.
Variable Definitions
- R
- Nominal annual interest rate (the quoted rate).
- n
- Number of compounding or payment periods per year.
- i
- Periodic interest rate.
- A
- Loan amount (principal).
- P
- Amount of each equal payment.
- N
- Total number of payments (loan term).
Calculation Steps Explained — Fig. 2
- How do you calculate the number of payments required to repay a loan?
To calculate the number of payments needed to repay a loan, apply the loan amortization formula with logarithmic operations. This method assumes fixed periodic payments and a constant interest rate. The following example illustrates the process:
- Calculate the periodic interest rate by dividing the annual rate
R = 6%by the number of periods per yearn = 12:i = 0.005. - Substitute the values into the repayment formula:
N = -ln(1 - iA/P) ÷ ln(1 + i), whereA = 50,000,P = 1,000, andi = 0.005. - Evaluate the ratio:
iA/P = (0.005 × 50,000) ÷ 1,000 = 0.25. Thus,1 - 0.25 = 0.75. - Compute the natural logarithm:
ln(0.75) ≈ -0.2876820724…. Apply the negative sign:-ln(0.75) ≈ 0.2876820724…. - Evaluate the denominator:
ln(1.005) ≈ 0.0049875415…. - Divide the values:
N ≈ 0.2876820724… ÷ 0.0049875415… ≈ 57.6801…. - Round to the nearest whole payment period: N ≈ 58.
This means 58 monthly payments of $1,000 are required to repay a $50,000 loan at a 6 % annual interest rate, compounded monthly.
- Calculate the periodic interest rate by dividing the annual rate
Step-by-step Solution – Fig. 2
i = 0.06 ÷ 12 = 0.005N = -ln(1 - (0.005 × 50,000 ÷ 1,000)) ÷ ln(1.005)= -ln(1 - 0.25) ÷ ln(1.005)= -ln(0.75) ÷ ln(1.005)≈ -(-0.2876820724…) ÷ 0.0049875415…≈ 0.2876820724… ÷ 0.0049875415…≈ 57.6801…≈ 58
Final Answer
The final answer (N) is approximately 57.6801…. Because partial payment periods are not possible, we round up to 58.
Validate the calculator. $50,000 loan at 6 % annual rate with $1,000 monthly payments.
| Loan Amount: | 50,000.00 |
|---|---|
| Number of Payments (#): | = 58 |
| Annual Interest Rate: | 6.0 % |
| Payment Amount: | 1,000.00 |
| Payment Frequency: | Monthly |
| Compounding: | Monthly |
| Amortization Method: | Normal |
Notes:
- This example uses the same calculation shown in Fig. 2.
- The equation assumes fixed payments and equal-length periods. If you do not obtain the same result, confirm that the loan date and first payment due date (on the
Optionstab) are exactly one month apart, and ensure no extra payments are entered. - The equation provides a guideline. Rounding down to 57 payments will make the last payment larger than if you use a full 58-payment term.
Loan Amount Equation — Calculate the Amount You Can Borrow (PV)
Fig. 4 – Step-by-step solution of the loan amount equation.
Variables: R = 6 %; f = 12; n = 60; PMT = 1,000.
Variable Definitions
- R
- Nominal annual interest rate (the quoted annual rate).
- i
- Interest rate per period (
Rdivided byf). - f
- Number of payment periods per year.
- n
- Total number of payments for the loan or investment.
- PMT
- Amount of each equal periodic payment.
- PV
- Loan amount, or present value — the amount you can borrow.
Calculation Steps Explained — Fig. 4.
- How do you calculate how much you can borrow based on a fixed payment?
To determine the loan amount you can borrow when the monthly payment, interest rate, and loan term are known, use the present value formula for an ordinary annuity. The process with example values is as follows:
- Compute the periodic rate from the annual rate:
i = R ÷ f = 0.06 ÷ 12. - Evaluate the periodic rate:
i = 0.005. - Substitute into the formula:
PV = 1,000 × [(1 − (1 + 0.005)−60) ÷ 0.005]. - Simplify the base inside the exponent:
1 + 0.005 = 1.005. Result:PV = 1,000 × [(1 − (1.005)−60) ÷ 0.005]. - Evaluate the power term:
(1.005)−60 ≈ 0.741372196…. - Subtract from
1and divide by the rate:(1 − 0.741372196…) ≈ 0.258627804…; then ÷0.005. - Evaluate the bracketed factor:
≈ 51.7255608…. - Multiply by
1,000to obtain the unrounded present value:≈ 51,725.5608…. - Round to cents for currency reporting: PV ≈ $51,725.56.
This result means that a borrower making 60 monthly payments of $1,000 at a 6 % annual interest rate, compounded monthly, could borrow approximately $51,725.56.
- Compute the periodic rate from the annual rate:
Step-by-step Solution – Fig. 4
i = 0.06 ÷ 12= 0.005PV = 1,000 × [(1 − (1 + 0.005)−60) ÷ 0.005]= 1,000 × [(1 − (1.005)−60) ÷ 0.005]≈ 1,000 × [(1 − 0.741372196…) ÷ 0.005]≈ 1,000 × [0.258627804… ÷ 0.005]≈ 1,000 × 51.7255608…≈ 51,725.5608…≈ 51,725.56
Final Answer
The final answer for the loan amount (PV) is approximately 51,725.56.
Validate the calculator. 60-month loan at 6 % annual rate with $1,000 monthly payments.
| Loan Amount: | = 51,725.56 |
|---|---|
| Number of Payments (#): | 60 |
| Annual Interest Rate: | 6.0 % |
| Payment Amount: | 1,000.00 |
| Payment Frequency: | Monthly |
| Compounding: | Monthly |
| Amortization Method: | Normal |
Notes:
- This example uses the same calculation shown in Fig. 4.
- The loan amount equation assumes that all periods are equal in length and that the payment amount remains fixed.
Annual Interest Rate Equation — Calculate the Interest Rate (R) for a Loan
Fig. 6 – Step-by-step solution of the annual interest rate equation using a closed-form expression.
Variables: PMT = 938.99; n = 60; P = 50,000; f = 12.
Variable Definitions
- PMT
- The fixed payment amount.
- n
- Total number of payments (loan term).
- P
- Loan principal (initial borrowed amount).
- f
- Number of payments per year (payment frequency).
- r
- Periodic interest rate (decimal form).
- R
- Nominal annual interest rate (percentage).
Calculation Steps Explained — Fig. 6
- How do you calculate the interest rate based on known payment and loan values?
To calculate the periodic interest rate from known loan terms, use the present value formula and apply an iterative method such as Newton–Raphson. This method refines the interest rate until the calculated loan value matches the target. Example:
- Set up the net present value equation using the annuity factor:
NPV(r) = 938.99 × (1 − (1+r)−60)/r − 50,000. - Choose an initial guess for the rate:
r₀ = 0.005. - Evaluate the annuity factor at
r₀:((1 − (1+r₀)−60)/r₀) ≈ 51.7255607511…. - Form the residual at
r₀:f(r₀) ≈ 938.99 × 51.7255607511… − 50,000. - Compute:
≈ 48,569.7842897054… − 50,000. - Residual:
≈ −1,430.2157102946…. - Evaluate the derivative at
r₀:f′(r₀) ≈ −1,401,824.5767294535…. - Apply Newton’s update:
r₁ = r₀ − f(r₀)/f′(r₀) ≈ 0.0039797470…. - Evaluate the annuity factor at
r₁:((1 − (1+r₁)−60)/r₁) ≈ 53.2803574944…. - Residual:
f(r₁) ≈ 938.99 × 53.2803574944… − 50,000. - Compute:
≈ 50,029.7228836692… − 50,000. - Residual:
≈ 29.7228836692…. - Derivative:
f′(r₁) ≈ −1,460,553.6747891533…. - Next update:
r₂ = r₁ − f(r₁)/f′(r₁) ≈ 0.0040000974…. - Evaluate annuity factor at
r₂:((1 − (1+r₂)−60)/r₂) ≈ 53.2487163871…. - Residual:
f(r₂) ≈ 938.99 × 53.2487163871… − 50,000. - Compute:
≈ 50,000.0122003501… − 50,000. - Residual:
≈ 0.0122003501…. - Derivative:
f′(r₂) ≈ −1,459,354.8371115437…. - Next update:
r₃ = r₂ − f(r₂)/f′(r₂) ≈ 0.0040001058…. - Evaluate annuity factor at
r₃:((1 − (1+r₃)−60)/r₃) ≈ 53.2487033941…. - Residual:
f(r₃) ≈ 938.99 × 53.2487033941… − 50,000. - Compute:
≈ 50,000.00000000206… − 50,000. - Residual:
≈ 0.000000002058…. - Derivative:
f′(r₃) ≈ −1,459,354.3448535450…. - Final Newton correction:
r ≈ r₃ − f(r₃)/f′(r₃) ≈ 0.004000105796…. - Convert to nominal annual rate:
R = r × 12 ≈ 0.04800126955…. - Express as a percentage (to four decimals): R ≈ 4.8001 %.
This result shows that the loan carries a nominal annual interest rate of approximately 4.8001 %, based on 60 monthly payments of $938.99 to repay $50,000.
- Set up the net present value equation using the annuity factor:
Step-by-step Solution – Fig. 6
NPV(r) = 938.99 × (1 − (1+r)−60)/r − 50,000r₀ = 0.005((1 − (1+r₀)−60)/r₀) ≈ 51.7255607511…f(r₀) ≈ 938.99 × 51.7255607511… − 50,000≈ 48,569.7842897054… − 50,000≈ −1,430.2157102946…f′(r₀) ≈ −1,401,824.5767294535…r₁ = r₀ − f(r₀)/f′(r₀) ≈ 0.0039797470…((1 − (1+r₁)−60)/r₁) ≈ 53.2803574944…f(r₁) ≈ 938.99 × 53.2803574944… − 50,000≈ 50,029.7228836692… − 50,000≈ 29.7228836692…f′(r₁) ≈ −1,460,553.6747891533…r₂ = r₁ − f(r₁)/f′(r₁) ≈ 0.0040000974…((1 − (1+r₂)−60)/r₂) ≈ 53.2487163871…f(r₂) ≈ 938.99 × 53.2487163871… − 50,000≈ 50,000.0122003501… − 50,000≈ 0.0122003501…f′(r₂) ≈ −1,459,354.8371115437…r₃ = r₂ − f(r₂)/f′(r₂) ≈ 0.0040001058…((1 − (1+r₃)−60)/r₃) ≈ 53.2487033941…f(r₃) ≈ 938.99 × 53.2487033941… − 50,000≈ 50,000.00000000206… − 50,000≈ 0.000000002058…f′(r₃) ≈ −1,459,354.3448535450…r ≈ r₃ − f(r₃)/f′(r₃) ≈ 0.004000105796…R = r × 12 × 100 ≈ 4.800126955…R ≈ 4.8001 %
Final Answer
The final answer for the annual interest rate (R) is approximately 4.8001 %.
Validate the calculator. $50,000 loan with $938.99 monthly payments for a 60-month term.
| Loan Amount: | 50,000.00 |
|---|---|
| Number of Payments (#): | 60 |
| Annual Interest Rate: | = 4.8001 % |
| Payment Amount: | 938.99 |
| Payment Frequency: | Monthly |
| Compounding: | Monthly |
| Amortization Method: | Normal |
Notes:
- Why an iterative method is required.There is no algebraic (closed-form) solution for the interest rate when the payment, term, and loan amount are known. The rate appears in both exponents and denominators, so it must be found using a numerical method that refines the estimate through repeated steps.
- Displayed values are shortened for clarity.To improve readability, decimal values shown in each step are shortened. However, all calculations use high-precision values. If verifying results independently, use at least 12 decimal places for the periodic rate and full calculator or software precision for intermediate steps (do not round between steps).
- How the rate is refined at each step.Each iteration uses the current estimate, the function value, and its slope (derivative) to compute a better estimate:
rk+1 = rk − f(rk) ÷ f′(rk). This continues until the estimate stabilizes. - About the algorithm used to find the interest rate.The calculation uses the Newton–Raphson method, a standard numerical algorithm widely used in finance. It finds the periodic rate that sets the net present value (NPV) of cash flows to zero—the internal rate of return (IRR).
- You can verify the calculated interest rate by using it to recompute the payment or loan amount. If the recomputed value differs by no more than a few cents, the rate is considered accurate. Minor differences may occur due to rounding the displayed rate to four decimal places.
Payment Amount Equation — Calculate the Periodic Payment Amount
For step-by-step guidance on solving the payment equation, seeAmortization Schedule — Payment Calculation Steps.
Amortization Equation — Calculate the Amortization Schedule
Normal amortization, for any period: ending balance = beginning balance + periodic interest − payment.
For step-by-step guidance on solving this equation, seeAmortization Schedule — Calculation Steps.
Conclusion
Over several decades, I have discussed loan details with users, including loans structured with unusual features. Based on that experience, I believe the loan calculators on this site can generate schedules for any structured settlement loan. If you have a loan with special requirements, please ask.

NK says:
There seems to be no obvious way to use a different currency
Karl says:
Click in the lower right corner of any calculator on the “$ : MM/DD/YYYY.” That will cause a window to open that will let you select a currency and date format. Or, click on the menu choice “More” and select “Set Currency and Date Format.”
Hope this helps.
Faizan Asif says:
This is a clean and intuitive interface! One small suggestion: it would be great to have an option to select a different currency for international users. Everything else works smoothly—nice job!
Karl says:
The user can change the currency!
In the lower right corner of any calculator, please click on “$ : MM/DD/YYYY”. This will open a window that gives visitors the ability to pick from over ninety currencies and six date format conventions!