All About Loan Amortization
What is Loan Amortization?
To paraphrase Wikipedia: loan amortization refers to the process of paying off a loan over time through scheduled, recurring payments. Each payment consists of two parts: a portion that covers interest accrued since the last payment, and a portion that reduces the loan’s principal balance.
An amortization schedule is a report that shows how each payment is allocated between principal and interest. It also shows the remaining loan balance after each payment. A schedule may be forward-looking (a projection based on assumptions), or it may document actual payment history.
This website provides calculators that support both projected and actual amortization schedules. (See the listing in the left-hand column.)
This page explains how amortization works, what to consider before borrowing, and which loan terms can reduce total repayment costs. It’s not just about getting the lowest interest rate.
Topics covered (click to jump):
For accurate amortization calculations, a calculator must allow the user to set both the loan origination date and the first payment due date independently.
Why does this matter?
The time between when the loan originates (the "closing date") and when the first payment is due is almost never equal to the selected payment frequency. For example, if payments are monthly, the first period will likely be slightly shorter or longer than one month. This difference is commonly called an odd-length first period or stub-period.
Supporting odd-length first periods enables more accurate calculations—but it also means your results may differ from other calculators that do not handle this correctly.
Long first period
A long first period occurs when the time between the loan date and the first payment date exceeds the chosen payment frequency. Example: loan originates on May 16 and the first payment is due July 1 (assuming monthly payments). Interest for the additional days can be handled in four different ways:

- None – no interest charged for the extra days (not realistic, but supported)
- With first – odd-day interest is added to the first payment, which will be higher than future payments
- With origination – odd-day interest is paid at loan origination (commonly called prepaid interest)
- Amortized – odd-day interest is spread evenly across all payments; the calculator increases each payment slightly

Short first period
A short first period occurs when the time between the loan date and the first payment is less than the selected payment frequency. There are three ways to handle this:
- No payment reduction – the calculator uses a full, standard payment amount for the first payment; the final payment is reduced to compensate
- Reduce first – the first payment is reduced to reflect the short period
- Reduce all – all payments are slightly reduced to compensate for the shorter first period

Here’s a more formal definition of odd-day interest from the Financial Dictionary.
One more important note about dates:
By default, amortization schedules typically report annual totals as of December 31.
However, some taxpayers have different fiscal year-ends. A well-designed calculator should allow users to set year-end totals to any month of the year.

There are many calculators hosted here at AccurateCalculators.com that support stub-periods, and odd day interest due to long or short initial periods.
Nine Loan Amortization Methods

Normal Loan Amortization
If you're unsure which option to select, use this one. In the U.S., nearly all loans use the "normal" amortization method.
Here are the defining features of a normal loan or mortgage:
- They have level payments; that is, the scheduled payment amount remains the same for each period (except possibly for odd-day interest, as discussed above).
- The interest paid each period declines over time as the principal balance is reduced.
- To keep payments level, the portion applied to principal increases with each installment.
- There may be a slight adjustment ("rounding") on the final payment to reduce the balance to zero.
The next method is one most consumers should avoid.
Rule-of-78s Payment Schedule
The Rule-of-78s method front-loads interest. This means the borrower pays more interest at the beginning of the loan term and less toward the end—compared to a normal amortization schedule.
Importantly, both the total interest paid and the periodic payment amount are the same as with a "normal" loan. The only difference lies in the allocation of interest vs. principal over time.
This blog post explains Rule-of-78s amortization in detail and why you may want to avoid this type of loan.
Next up: the amortization method that offers the lowest periodic payment. There’s only one catch…
Interest-Only Amortization
Some loans require the borrower to pay only the interest due each period. These are known as “interest-only loans.”
Here are the typical characteristics of an interest-only loan or mortgage:
- The periodic payment amount generally stays the same.
- The interest amount remains constant because the loan balance doesn’t decrease.
- The entire principal balance, plus interest for the final period, is due with the last payment.
If you think interest-only loans aren’t very common, think again.
Many bonds sold to investors are structured as interest-only loans. Bond buyers are lending money to the issuer, and the bonds pay a periodic coupon—representing interest only. According to the Securities Industry and Financial Markets Association (SIFMA), the U.S. bond market—excluding mortgage- and asset-backed securities—reached $47.4 trillion in Q1 2025, a 5.1% increase over the previous year.
That’s a lot of debt financed with interest-only payments!
If you represent a bond issuer, you can create a bond coupon payment schedule using this site's amortization calculator. Enter the “loan date” as the bond’s issuance date and the “first payment date” as the first coupon payment. Then select the “Interest-Only” amortization method.

No Interest Loan Amortization
Yes, it happens! I added this amortization method to the Windows version of my calculators more than 20 years ago. Someone called me (remember phone calls?) and explained that he and his wife were lending money to their son and needed a payment schedule they could agree on—without charging interest.
Many calculators on this site still support interest-free loans.
You might ask, “Why not just enter a 0% interest rate?”
Here’s why: if a user enters “0” for any input, the calculator interprets it as an unknown value and attempts to solve for it. So entering 0% as the interest rate triggers the calculator to try to calculate the rate.
To avoid this, simply select the “No Interest” amortization method.

The next amortization method can save you money—if you can afford the higher initial payments.
Fixed Principal Loan Table
Before digital tools were widely available, lenders often used the fixed principal amortization method. Why? Because it was simple to calculate without needing a calculator or computer.
The payment is calculated by dividing the loan principal by the number of payments in the term and then adding the interest due for that period.
Here are the characteristics of a fixed principal loan or mortgage:
- Payments start out higher than with a “normal” loan.
- The payment amount declines over time as interest charges decrease with the loan balance.
- The principal portion of each payment is fixed. For example, with a $1,200 loan and a one-year term, the principal portion will always be $100 per month.
- The borrower pays less total interest.
- The final payment may include a rounding adjustment to reduce the balance to zero.

(Note the declining payment amount)
Canadian Amortization Schedule
The Canadian amortization method is the same as the "normal amortization method" with one key difference: when selected, the calculator automatically sets the payment frequency to monthly and the compounding frequency to semiannual.
Typically, a conventional loan uses the same frequency for both payments and compounding.
Because the Canadian method compounds interest less frequently, it results in a slightly lower scheduled payment. That’s because the total interest accrued each period is somewhat less than with monthly compounding.
For more background, see A Guide to Mortgage Interest Calculations in Canada.
Amortization with a Balloon Payment
Sometimes, loan terms call for monthly payments based on a long amortization period—say, 30 years—but the loan itself matures much sooner, such as in five years.
In this case, even after five years of regular payments, a significant loan balance remains. That balance, due in full at the end of the loan term, is the balloon payment.
Creating an amortization schedule that includes a balloon payment is simple using this calculator.
- First:
- Enter the loan amount.
- Enter the annual interest rate.
- Enter the number of payments used to calculate the monthly payment—for example, 360 (30 years × 12 months).
- Enter “0” for the payment amount and click “Calc.” The calculator will solve for the monthly payment.
- Then:
- Change the number of payments to the actual loan term—e.g., 60 for a five-year term.
- Click “Print Preview” to view the amortization schedule, including the balloon payment.

Loan Schedule with Points, Fees and APR Support
Some loans require the borrower to pay an upfront charge called "points."
Why would a borrower be willing to pay an extra charge?
When the borrower pays points, the lender reduces the loan’s interest rate. Points are essentially prepaid interest (and the IRS treats them that way). One point equals 1% of the loan amount—so one point on a $300,000 loan would cost $3,000.
The calculator provides two ways to incorporate points into the amortization schedule. Click "Settings" and select "Points, Charges & APR Options."
If "Include dollar value of points in interest charges" is checked, the calculator shows the points paid at origination and includes their cost in the total interest paid over the life of the loan.
If the box is unchecked, the dollar value of the points is shown in the report header only and does not affect the interest totals.
For more on how points work, see Moving.com’s explanation of mortgage loan points.
Points affect the loan’s APR. If you want to calculate the APR (and you should if you're the borrower), the calculator can include a Truth-in-Lending Act-compliant APR disclosure at the end of the schedule. Just check the box for "Include Regulation 'Z' APR Disclosure calculation at the end of the schedule?" and be sure to enter any relevant fees in the "Other charges & fees (for APR calculation)?" field.

Negative Amortization Calculation
Users frequently tell me they use this site's calculator to “check their lender’s payment amount.”
That’s fine—but borrowers should understand there’s no such thing as the "correct" payment amount. The only amount that matters is the one agreed upon by both borrower and lender. If the lender quotes $315 and the borrower expects $311, that’s not a problem—so long as they agree on how interest is being calculated.
If the parties agree on the interest calculation, paying slightly more than expected may shorten the loan term or reduce the final payment. The result? A bit less interest paid over the life of the loan.
So what does this have to do with negative amortization?
Simple: if the agreed-upon payment is not large enough to cover the interest due, the loan will negatively amortize.
This amortization calculator allows you to enter any payment amount—even one that’s too small to cover interest. If that happens, it will create a negative amortization schedule automatically.
When the payment is less than the interest due, the unpaid interest is added to the loan balance, causing it to grow over time.
There’s nothing inherently wrong with negative amortization. But borrowers need to be prepared to make a much larger final payment that includes the accumulated unpaid interest.
If you're considering such a loan, check the last payment line in the schedule. That row shows the lump-sum final payment you'll owe—including any unpaid interest.
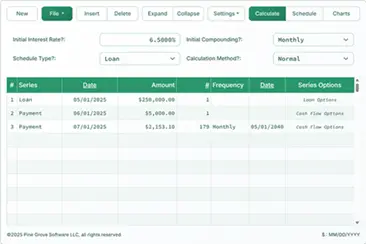
See the negative principal values in the example below.

What Do You Think?
Or what would you like to learn more about?
This page covers a great deal about amortization schedules—but of course, it can't address every scenario.
Let me know in the comments below if there’s something I missed. You're also welcome to ask questions, and I’ll do my best to answer them promptly and accurately.
Melanie says:
I am trying to get an amortization schedule of a loan to my business. I am loaning it money and charging interest (as required by the IRS) but don’t expect a repayment to start for five years. I then will expect a standard loan- like a mortgage- with monthly payments. How do I input that 5 year no-payment time, while still charging interest as required?
Melanie says:
I sent a question but have since figured out the answer. Thank you for this excellent tool!
Karl says:
You’re welcome! I’m happy the site met your needs.
Rob says:
I am looking through your amortizations and need help. Looking for an amortization based on 360 days for commercial loan. Can you help direct me if you have one available?
Thanks
Rob
Karl says:
Do you just want to create amortization schedules? This loan calculator support 360 day years and will create an amortization schedule. See the options tab to set the days per year.
Stephen M Brennan says:
I have a $1.25M loan, 60 month term, 6.5% compounded daily, with a closing date of 12/12/19. First payment of P&I is not due until 2/1/10. Borrower will pay an additional $11,284.56 interest payment on 2/1/20 to cover the interest only period from 12/12/19 – 2/1/20. How do I set this up in your calculator so I can print out an amortization schedule?
Karl says:
What you have is what we call a long initial period – that is, the time between the loan origination and the first payment is longer than the scheduled payment frequency.
This calculator, and many on this site, give the user options for how to handle this scenario. It sounds as if you want the extra interest paid with the first payment. On the "Options" tab, select "With First", it that’s the case.
Note, the total amount will vary depending on how the days per year option is set and how the compounding frequency is set. I mention this because I’m not sure how you calculated $11,284.
Tammy says:
I have been asked to do an amortization schedule for a commercial property sold in June, 2001 & I am assuming the payments started the following month. According to several prior year tax returns, the beginning balance is $350,000 with commissions and expenses of sale of $5,771. On the tax returns that I have, 2014-2018, the interest amount paid each year is the same @ $22,579. The remaining principle balance at the end of 2018 is $223,770. Payment amount each month is $2,413.86. Is this the correct way to calculate this? Thanks for your help with this.
Karl says:
What are you trying to calculate? The current principal balance? Without knowing the terms of the loan and the payments paid, you can’t accurately calculate the balance due. What I find questionable is, since the principal amount is apparently declining, why is the interest amount the same each year. As a loan amortized, the interest amount declines each year, and the amount applied to principal increases.
Unless the monthly payment amount due is also decreasing. In that case, the terms are a fixed principal amount.
Bob Cranston says:
I have a commercial client who borrows money with a daily payment for five days a week. He borrows $40,000 on Monday, and his first payment is on Tuesday. But no payments are due on the weekends. So he has five payments a week. How can I calculate this? I’ve tried daily, but it gives me a 342% interest rate. Trying weekly gives me a 248% interest rate. I’ve tried compounding daily and weekly; that what gets me those interest rates. What other options are there?
Karl says:
Is it the nominal annual interest rate that you want to calculate?
This calculator should be able to do it (without knowing the payment amount). It will solve for the interest rate and it will also allow you to set up skipped payments – under "cash flow options."
If you try it, scroll down the page to the tutorials.
And once there, if you have any questions, just ask.
Harold says:
There is a type on this page “first payment is due on July 1st (ssuming”. Missing an “a” in assuming.
Karl says:
Thanks. Fixed. (Reread your first sentence. 🙂
Harold says:
I re-read my first sentence. Oops, I made a typo too!
Sandie says:
I have a loan with the following terms:
Loan amount 1,717,000
Annual Interest Rate 1%
Loan Origination Date 04/21/20
First payment due 03/21/21
accrued interest from 04/21/20-02/21/20 is paid at the end of the loan
14 monthly installments
Last payment on 04/21/20 to include interest from deferral period.
Payments (with the exception of the last one) are equal
Interest calculated on 360 year x number of days elapsed
Karl says:
Sorry Sandie, but I do not have a calculator that will handle deferred interest as you describe it. My guess, if one exists, it will be a feature of a loan servicer’s program that has an interest deferral feature.
Quintin says:
I have a borrower whose note is $59,500 for 15 years at 7%.
Payment is due on the 15th, but he pays on the 12th, 9th, 11th etc. How do I calculate those early payment credits in a chart that automatically adjusts each column?
Karl says:
You’ll need to use a different calculator. Please use this payoff calculator. It lets the user record the payments on the actual dates paid.
emmanuel says:
hello there!
i need assistance with this questions in loan amortization. my dad wants to borrow a business loan.
Supposing he borrowed $30, 000 and he has arranged for 9 year amortized loan with a monthly interest rate of 4%.
a) What will his monthly payment be? b) After 5 years, what will the balance be? c) How much interest will he have paid after the 5 years? d) What will be his total interest paid at the end of the 9 years?
Karl says:
Hi, this calculator will give you all the numbers you want. However, do you really mean the interest rate is 4% a month? If so, to use this calculator, you’ll need to convert the rate to an annual rate – 48%. Now answer the questions the calculator asks, and view the schedule using the "Print Preview" feature.
emmanuel says:
Thanks Karl!
when converting the monthly interest of 4% to an annual rate, is it -48% or just 48%???
Karl says:
You’re welcome. If the monthly interest rate is quoted as a positive value, then the annual rate would also be a positive value.